Коды Хемминга. Ознакомление с принципами построения кодов Хэмминга

Министерство образования и науки РФ

Новосибирский государственный технический университет

Кафедра ВТ

Лабораторная работа № 2

по дисциплине «Кодирование и передача данных»

«Коды Хемминга»

Факультет: АВТ                                   Преподаватель:                                   Титов Г. И.

Группа: АМ-310

Студенты: Сергиенко С.А.

              Бондарь А.В.

              Чадов К.С.

Новосибирск, 2006

1. Цель работы.

Ознакомиться с принципами построения кодов Хэмминга, их свойствами и способами реализации кодирующих и декодирующих устройств.

Исследовать системы передачи данных для обнаружения и исправления ошибок, в которых используются коды Хэмминга.

2. Выполнение.

Граф схема алгоритма функции кодирования

 

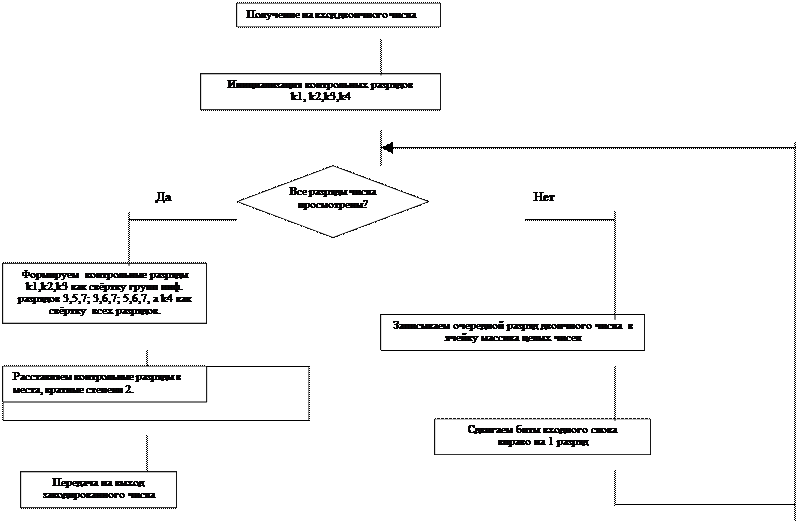Рис. 1. ГСА функции encode

Исходный текст функции encode

char encode(char value)

{         

 int k1=0,k2=0,k3=0,k4=0;

char temp;

int A[8];

temp=value;

for(int i=0;i<8;i++)

{

if(temp&1) A[i]=1;

       else A[i]=0;

       temp=temp>>1;

}

k1=(A[2]+A[4]+A[6])%2;

k2=(A[2]+A[5]+A[6])%2;

k3=(A[4]+A[5]+A[6])%2;

k4=(k1+k2+A[2]+k3+A[4]+A[5]+A[6])%2;

value=value^(k1)^(k2*2)^(k3*8)^(k4*128);

return value;}

Формируем синдром ошибки k и контрольный разряд k4 как свёртку всех разрядов.

Да

Нет

Инициализация контрольных разрядов

Получение на вход двоичного числа

Граф схема алгоритма функции декодирования

Рис. 2. ГСА функции decode

Исходный текст функции decode

 

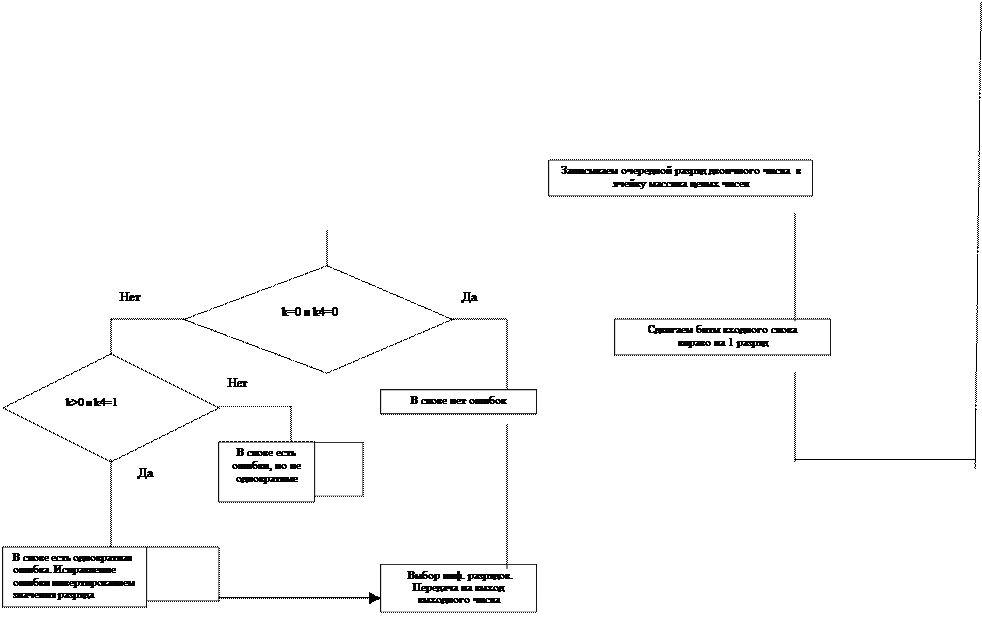
Рис. 2. ГСА функции decode

Исходный текст функции decode

сhar decode(char value)

{

 int k=-1;

int k1=0,k2=0,k3=0,k4=0;

char temp;

int A[8];

temp=value;

     for(int i=0;i<8;i++)

     {

      if(temp&1) A[i]=1;

       else A[i]=0;

       temp=temp>>1;

     }

k1=(A[0]+A[2]+A[4]+A[6])%2;

k2=(A[1]+A[2]+A[5]+A[6])%2;

k3=(A[3]+A[4]+A[5]+A[6])%2;

k4=(A[0]+A[1]+A[2]+A[3]+A[4]+A[5]+A[6]+A[7])%2;

k=k1+k2*2+k3*4-1;        //Синдром ошибки

if(k==-1 && k4==0)       //нет ошибки

{ value=A[2]*4+A[4]*16+A[5]*32+A[6]*64; return value;}

if(k>=0 && k4==1)                //Однократная ошибка

  {

    if(A[k]==0) A[k]=1;          //Исправление ошибки

    else A[k]=0;

    value=A[2]*4+A[4]*16+A[5]*32+A[6]*64; return value;

  }

return value;

}

3. Выводы

Модифицированный код Хемминга позволяют исправлять одинарную ошибку и отслеживать наличие двойной ошибки.

При работе с программой было обнаружено, что в части программы, изображающей  результаты работы эталонной функции, в пункте отображаемой результат кодирования в десятичном коде отображается верное число, а в двоичном коде ошибочное. Было проверено на различных входных комбинациях и сделан вывод, что в исходном коде программы допущена ошибка: в двоичном коде отображается не закодированное число, а входная комбинация.