Кодирование по модифицированному коду Хэминга

Новосибирский государственный технический университет

Кафедра вычислительной техники

Лабораторная работа № 2

«Кодирование по модифицированному коду Хэминга»

Группа:  АМ-015

Студенты:     Вахтина Е.

                        Гаврилов Д.

                        Кивилёв Д.

                        Лыкова О.

Новоисбирск, 2003

1. Задание

            Разработать две функции code и decode, вставляемые в учебную программу «Стенд», реализующих кодировку и декодировку, соотвественно, 4-разрядных двоичных чисел, используя модифицированный код Хэмига.

2. Выполнение

Граф схема алгоритма функции кодирования

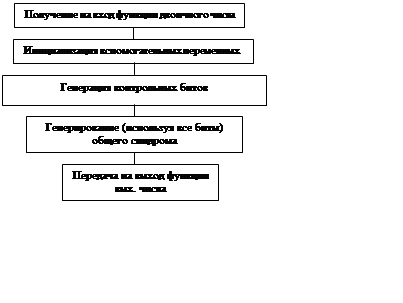
Рис. 1. ГСА функции code

Исходный текст функции code

char encode(char value)

{

//формат входного слова:

//биты   7  6  5  4  3  2  1  0

//            k0 a3 a2 a1 k3 a0 k2 k1

unsigned char mk=1;//маска

int i;

//Для простоты работы с входным словом производим преобразование формата вх.данных

bool a[8]; // в формат раб. данных, т.е. bool

for(i=0;i<8;i++,mk<<=1)

              a[i]=value&mk;

//индекс 0 массива соответствует 0-му разряду входного слова

//----генерируем контрольные биты----

a[0]=a[0]^a[2]^a[4]^a[6];

a[1]=a[1]^a[2]^a[5]^a[6];

a[3]=a[3]^a[4]^a[5]^a[6];

for(i=0;i<7;i++)//генерирование общего контрольного бита

    a[7]=a[7]^a[i];

//После всех преобразований и генераций необходимо результат преоьразовать в формат

char wrd=0;// выходных данных, т.е. в char

for(i=7;i>=0;wrd<<=1,wrd+=a[i--]);

    return wrd;

}

Граф схема алгоритма функции декодирования

Получение на вход функции двоичного числа

           

 

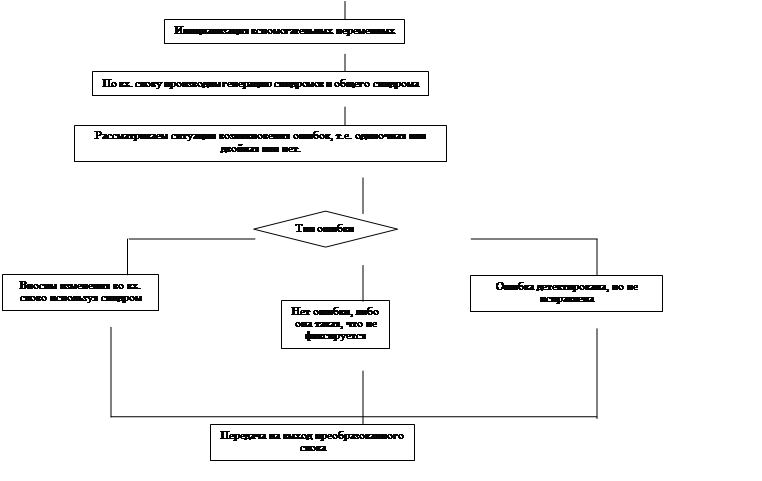Рис. 2. ГСА функции decode

Исходный текст функции decode

char decode(char value)

{

unsigned char mk=0x01;//маска

int i;

//----char value -> bool array a----

bool a[8];

for(i=0;i<8;i++,mk<<=1)

              a[i]=value&mk;

//----генерируем контрольные биты----

bool k[4]={0,0,0,0};//контрольные биты

k[0]=a[0]^a[2]^a[4]^a[6];

k[1]=a[1]^a[2]^a[5]^a[6];

k[2]=a[3]^a[4]^a[5]^a[6];

for(i=0;i<8;i++)//генерирование общего контрольного бита

              if(a[i]) k[3]=!k[3];

if( k[3] )

{//т.е. указана одиночная ошибка

              int r=0;//преобразовываем код места ошибки в десятичный

              int st=1;

              for(i=0;i<3;i++,st*=2)

              {

                            r+=st*k[i];

              }

              if(!r)

                            a[7]=!a[7];

              else

                            a[r-1]=!a[r-1];

}

if( (k[3]) | (!k[3]&!k[1]&!k[2]&!k[0]) )

{//нет ошибки или она одинарная

              a[0]=a[0]^a[2]^a[4]^a[6];

              a[1]=a[1]^a[2]^a[5]^a[6];

              a[3]=a[3]^a[4]^a[5]^a[6];

              for(i=0;i<8;i++)//генерирование общего контрольного бита

                            if(a[i]) a[7]=!a[7];

}

//если двойная ошибка, то оставляем таким же

//----bool array a -> char wrd----

char wrd=0x00;

for(i=7;i>=0;wrd<<=1,wrd+=a[i--]);

    return wrd;

//    return value;

}

3. Выводы

            Были разработаны алгоритмы кодирования и декодирования двоичных чисел. Результаты выполнения данных процедур совпадают с эталонными, что говорит о правильности работы алгоритмов. Конечно, одинарная ошибка детектируется и исправляется в отличии, от кодирования по паритету, но вот двойная ошибка только детектируется, тем более что может сложится такая ошибка, что она не будет детектирована (хотя, в принципе, это характерно для любого метода кодирования).