Определение внутригрупповых дисперсий, средней из внутригрупповых, межгрупповой и общей дисперсии

Тема 1. Сводка и группировка, средние величины, показатели вариации:

Задача 3. Производительность труда двух бригад (по 6 человек каждая) разных смен рабочих-токарей представлена в таблице:

Производство деталей за час, шт.
Бригада № 1 (I смена)	Бригада № 2 (II смена)
18	13
19	14
22	15
20	17
24	16
23	15

Определить: внутригрупповые дисперсии, среднюю из внутригрупповых, межгрупповую и общую дисперсии. Определить эмпирический коэффициент детерминации и эмпирическое корреляционное отношение. Сформулировать вывод.

РЕШЕНИЕ:

Рассчитаем внутригрупповые дисперсии.

Производство деталей за час,	Количество рабочих
	всего	в бригаде №1	в бригаде №2
13 14 15 16 17 18 19 20 22 23 24	1 1 2 1 1 1 1 1 1 1 1	- - - - - 1 1 1 1 1 1	1 1 2 1 1 - - - - - -
Итого:	12	6	6

Среднее производство деталей в бригаде №1: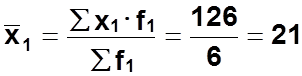

Внутригрупповая дисперсия по бригаде № 1

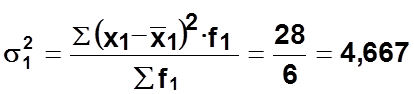
Среднее производство деталей в бригаде №2: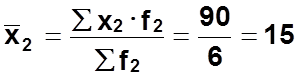

Внутригрупповая дисперсия по бригаде № 2

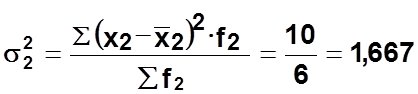
Средняя из внутригрупповых дисперсий:

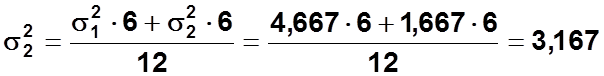
Расчёт межгрупповой дисперсии

Группы	Среднее производство деталей за час, шт,	Количество рабочих
1 2	21 15	6 6	3 -3	9 9	54 54
	Итого:	12			108

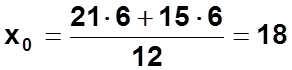
Межгрупповая дисперсия: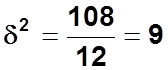

Расчёт общей дисперсии.

Производство деталей за час, шт,	Количество рабочих
13 14 15 16 17 18 19 20 22 23 24	1 1 2 1 1 1 1 1 1 1 1	13 14 30 16 17 18 19 20 22 23 24	-5 -4 -3 -2 -1 0 1 2 3 4 5	25 16 9 4 1 0 1 4 16 25 36	25 16 18 4 1 0 1 4 16 25 36
Итого:	12				146

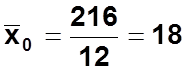
Общая дисперсия: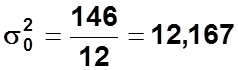

Правило сложения дисперсий:

 , где

;

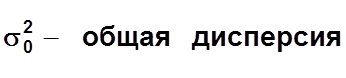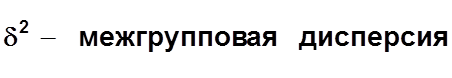
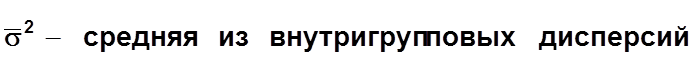
Эмпирический коэффициент детерминации:

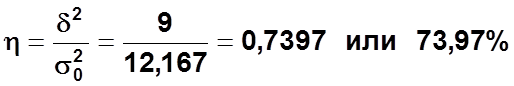
Эмпирическое корреляционное отношение:

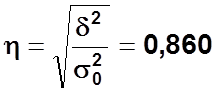
Вывод: 73,97% производительности рабочих обусловлены принадлежности к бригаде № 1 или № 2 и 26,03%  - влиянием других факторов.

Тема 2. Ряды динамики

Задача 4. Среднегодовая численность населения области выглядит сле­дующим образом:

Год	Среднегодовая численность населения, тыс. чел.
1992	2528,0
1993	2655,0
1994	2689,0
1995	2722,0
1996	2747,4

По этим данным:

1)  рассчитайте абсолютные (цепные и базисные) и средние показатели динамики. Результаты представьте в таблице;

2)   нанесите на график динамику ряда.

РЕШЕНИЕ

Заполним таблицу среднегодовой численности населения области.

год	Среднегодовая численность населен. обл. тыс. чел.	Абсолютный прирост, т		Темпы роста, %		Темпы прироста, %
		Цепной способ	Базисный способ	Цепной способ	Базисный способ	Цепной способ	Базисный способ
1992	2528,0	─	─	─	─	─	─
1993	2655,0	127,0	127,0	105,0	105,0	5,0	5,0
1994	2689,0	34,0	161,0	101,3	106,4	1,3	6,4
1995	2722,0	33,0	201,0	101,2	107,7	1,2	7,7
1996	2747,4	25,4	219,4	100,9	108,7	0,9	8,7

Средний уровень ряда динамики:

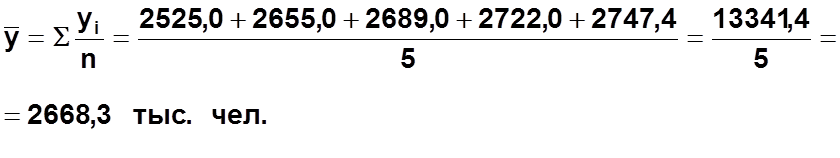
Средний абсолютный прирост:

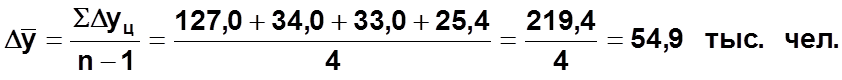
Средний темп роста:

Средний темп прироста:

Население области увеличивалось в среднем на 2,1% за год.

      среднегодовая

     численность

2750

 

2700

 

2650

2600

2550

 

2500

 

                    1992            1993            1994            1995            1996       года

Задача 6. Рассчитать прогноз объема перевозок на 2001 г. используя аналитическое выравнивание по прямой на основе следующих отчетных данных по грузовому автотранспортному предприятию:

показатель	1993	1994	1995	1996	1997	1998	1999	2000
Перевезено груза, тыс.т	436	430	420	422	400	400	372	360

РЕШЕНИЕ:

Проведём аналитическое выравнивание по прямой

Для упрощения расчётов заменим показатель Х - года условными годами: 1993 г. - -3 г.; 1994 г. - -2 г. …

Заполним расчётную таблицу