Сводка и группировка, средние величины, показатели вариации. Ряды динамики. Индексы

КОНТРОЛЬНАЯ РАБОТА ПО ТЕОРИИ СТАТИСТИКИ

заочной формы обучения 2009-10г.

ВАРИАНТ №12

Тема 1. Сводка и группировка, средние величины, показатели вариации:

Задача 1. Получены данные о возрастном составе туристической группы:

№ п/п	Возраст, лет		№ п/п	Возраст, лет
1	23		11	21
2	17		12	15
3	26		13	15
4	35		14	19
5	32		15	20
6	37		16	10
7	12		17	22
8	24		18	23
9	33		19	26
10	18		20	25

Требуется:

1) построить интервальный вариационный ряд распределения туристической группы по возрасту (образовав три группы равных возрастных интервалов);

2) построить гистограмму распределения, а также кумуляту, графически показать расположение моды и медианы;

3) определить показатели центра распределения (средний возраст группы (округляйте с точностью до 0,1), моду и медиану) и показатели размера и интенсивности вариации возраста в группе.

По полученным расчетам сформулировать вывод.

Решение

1) Используя комбинацию признаков, проведем группировку туристической группы по возрасту (образовав три группы равных возрастных интервалов).

Размах вариации

R = x_max – x_min = 37 – 10 = 27

Длина интервала:

h = i = R / k = 27 / 3 = 9 (лет)

Сгруппируем всех туристов (n = 20 чел.) в k = 3 группы интервалов, тем самым построим интервальный ряд распределения признака x_i – возраст, найдя по таблице число туристов, входящих в каждый интервал  (то есть, найдем частоты f_i), также рассчитаем некоторые необходимые для анализа вариации и структурных средних промежуточные показатели. Результаты расчетов занесем в рабочую таблицу.

Таблица

№ группы	Интервал* возраста, лет	Середина интервала, лет	Частота, чел.	Накопленная частота
	xi	x′i	fi	Si	x′i fi
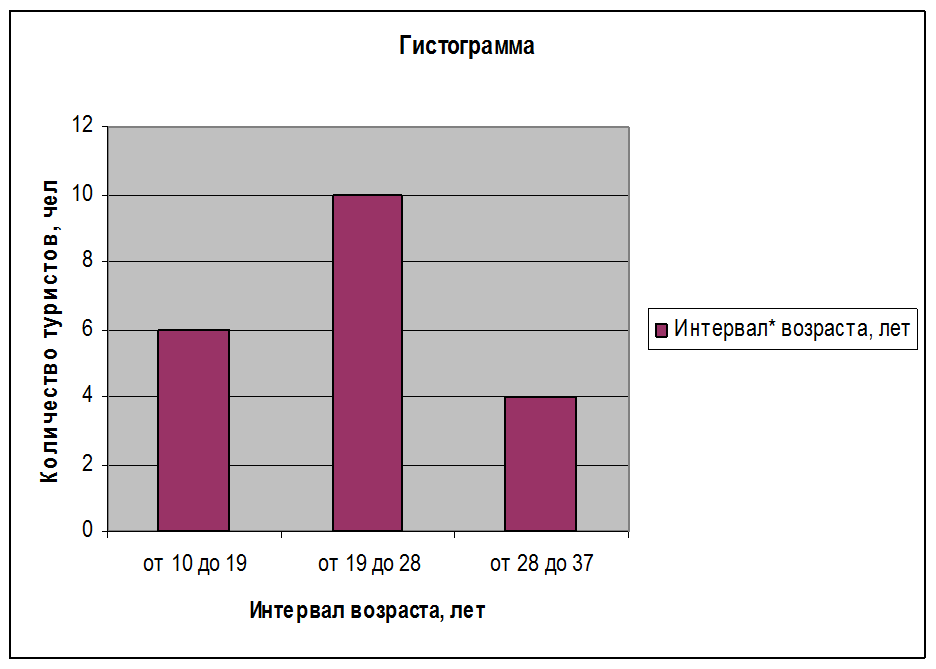
1	от 10 до 19	14,5	6	6	87
2	от 19 до 28	23,5	10	16	235
3	от 28 до 37	32,5	4	20	130
Итого			20

*Примечание: начало интервала входит в данный интервал, конец интервала входит в следующий интервал.

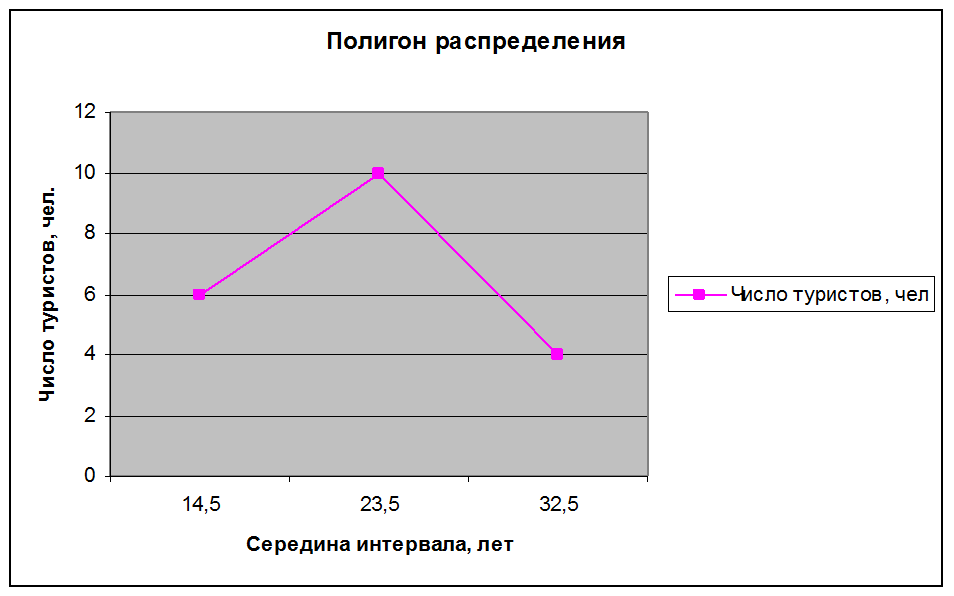
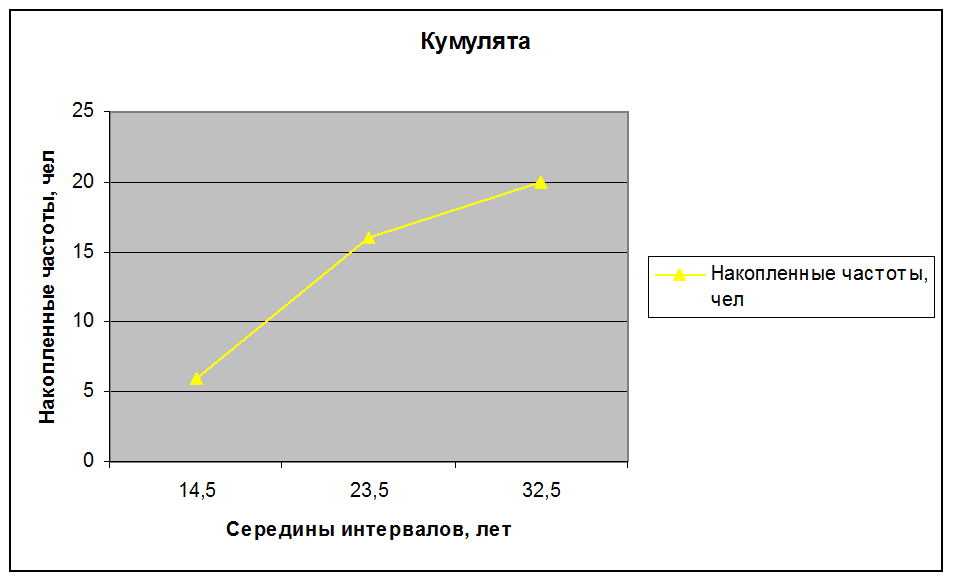
2) Построим гистограмму, полигон распределения работников по стажу работы, а также кумуляту:

3) определить показатели центра распределения (средний возраст группы (округляйте с точностью до 0,1), моду и медиану) и показатели размера и интенсивности вариации возраста в группе.

То есть рассчитаем такие показатели структуры распределения, как моду и медиану.

аналитически:

Мода — значение признака, наиболее часто встречающееся в изу­чаемой совокупности. В дискретном ряду модой является вариант с наибольшей частотой (частостью). В интервальном вариационном ряду мода рассчитывается по формуле:

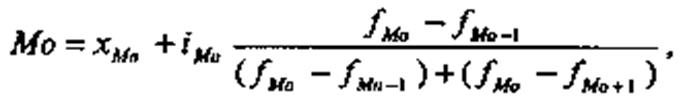
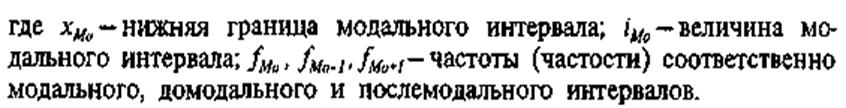
Модальный интервал — это интервал, имеющий наибольшую часто­ту (частость). В нашем примере это второй интервал — возраст от 19 до 28 лет.

Рассчитаем модальное значение признака, используя в качестве весов частоты распределения:

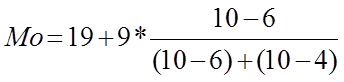 = 22,6 (года)

Таким образом, в нашем примере наиболее часто встречающаяся величина возроста составляет 22,6 года.

Отметим, что вычисление моды в интервальном ряду является весьма условным.

Медиана — вариант, расположенный в середине упорядоченного вариационного ряда, делящий его на две равные части, таким обра­зом, что половина единиц совокупности имеют значения признака меньше, чем медиана,  а половина — больше, чем медиана.  В интер­вальном ряду медиана определяется по формуле:

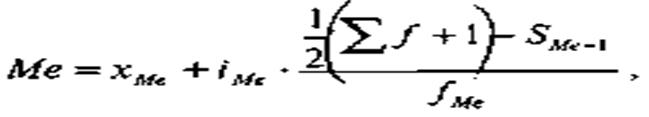
Для того чтобы найти медиану, предварительно рассчитывают накопленные частоты. Вариант, при котором накопилась половина численности совокупности, и есть медиана. По данным табл. находим ин­тервал, сумма накопленных частот в котором превышает  50%. Это второй интервал от 19 до 28 лет, он и является медиан­ным. Тогда

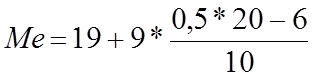= 22,6 (года)

Следовательно, половина туристов в нашем примере имеет возраст меньше 22,6 года, а половина — боль­ше этой величины.

Рассчитаем также среднее значение признака, используя модель        средней арифметической взвешенной для интервального ряда распределения 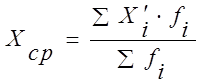            = 452 / 20 = 22,6 (года)

Показатели вариации.

  I.  Абсолютные

·  Размах вариации

R = 32,5-14,5=18 лет

Размах характеризует предельное отклонение значений признака.

·  Среднее линейное отклонение

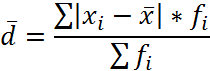
Расчеты представлены в таблице: