Другие предметы \ Статистика

Определение внутригрупповых дисперсий, средней из внутригрупповых, межгрупповой и общей дисперсии, страница 2

№

п/п

436

430

420

422

400

372

360

-3

-2

-1

-1308

-860

-420

400

800

1116

1440

Итого:

3240

1168

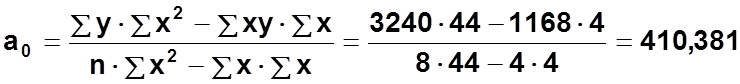
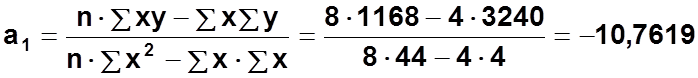
Рассчитаем прогноз перевозок на 2001 год (условный 5 год)

Задача 7. Имеются следующие данные о внутригодовой динамике ввода в действие жилых домов предприятиями всех форм собственности по кварталам:, млн.кв.м общей жилой площади.

квартал	1 год	2 год	3 год
I	2,1	2,2	2,4
II	4,2	5,1	5,0
III	4,1	3,9	4,8
IV	6,4	8,4	9,0

Определите индексы сезонности методом скользящей средней. Постройте график сезонной волны.

РЕШЕНИЕ:

Расчёт индексов сезонности методом скользящей средней

Год, квартал

Исходные

уровни

Скользящие средние

Сглаженные уровни с центрированием

1год I

III

2год I

III

3год I

III

2,1

4,2

4,1

6,4

2,2

5,1

3,9

8,4

2,4

5,0

4,8

9,0

16,8:4=4,2

16,9:4=4,25

17,8:4=4,45

17,6:4=4,4

19,6:4=4,9

19,8:4=4,95

19,7:4=4,93

20,6:4=5,15

21,2:4=5,3

4,225

4,350

4,425

4,650

4,925

4,940

5,040

5,225

0,970

1,471

0,497

1,097

0,792

1,700

0,476

0,957

Для получения средних индексов сезонности проводится осреднение исчисленных значений 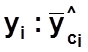по одноимённым кварталам

I кв: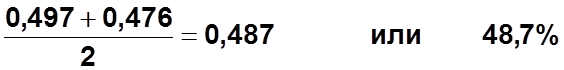

II кв: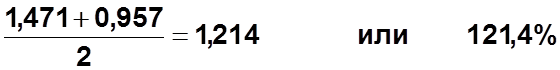

III 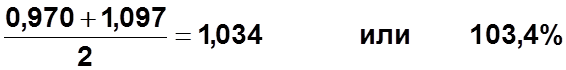кв:

IV кв:

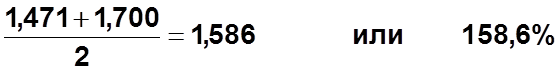
+60

+50 +58,6%

+40

+30

+20

+10 +21,4%

0 I кв. +3,4%

-10 II кв. III кв. IV кв.

-20

-30 -51,3%

-40

-50

Тема 8. Индексы

Задача 8. Выпуск продукции по заводу за два квартала следующий:

Вид продукции	Выпуск, тыс. шт.		Отпускная цена за шт., тыс.руб.
Вид продукции	I квартал	II квартал	I квартал	II квартал
А	26	20	4,8	5
В	28	30	7	7
С	34	40	6,5	6

Определить: 1) изменение (в%) выпуска каждого вида продукции, а также изменение выпуска продукции в целом по предприятию, 2) изменение (в%) цен по каждому виду продукции, а также изменение цен на продукцию в целом по предприятию.3) изменение (в%) сводного товарооборота. Определить влияние на изменение общего товарооборота: а) изменение объема, б) изменение цены.

РЕШЕНИЕ:

Продукцию А во II квартале выпустили на 23,1% меньше, чем в I квартале

Продукцию В во II квартале выпустили на 7,1% больше, чем в I квартале.

Продукцию С во II квартале выпустили на 17,6% больше, чем в I квартале.

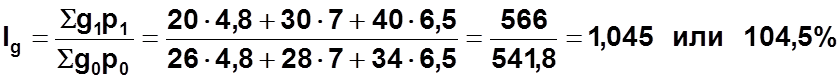
Выпуск продукции в целом по предприятию увеличился на 4,5%.

Цена на продукцию А во II квартале увеличилась на 4,2%.

Цена на продукцию В во II квартале не изменилась.

Цена на продукцию С во II квартале уменьшилась на 7,7%

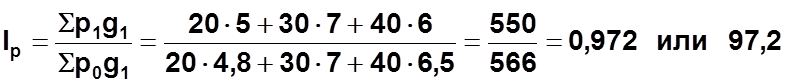
Цена на продукцию в целом по предприятию уменьшилась на 2,8%.

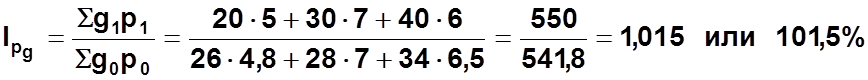
Сводный товарооборот увеличился на 1,5%

Определим влияние на изменение общего товарооборота

а) изменение объёма:

Общий товарооборот в результате изменения объёма увеличился на

24200 тыс.руб.

б) изменение цены

Общий товарооборот в результате изменения цены уменьшился на 16000 тыс. руб.

Задача 9. Известны следующие данные по перерабатывающему заводу:

Вид продукции	Общие затраты на производство в предшествующем году, млн.руб.	Изменение объема производства в натуральном выражении, %
А	250	+2,4
В	100	+4,5
С	200	-2,3
D	150	0

Сделайте сводную оценку увеличения производства продукции (в натуральном выражении), т.е. определите индекс физического объема реализации.

РЕШЕНИЕ:

Индекс физического объёма реализации равен

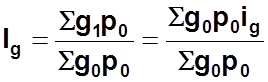
По условию индивидуальные индексы объёма производства равны

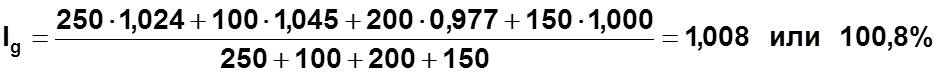
Объём производства (в натуральном выражении) увеличился на 0,8%.

Задача 10. Динамика себестоимости и объема производства двух предприятий характеризуется следующими данными:

Предпр.	Выработано прод. тыс.ед		Себестоимость единицы, руб.
Предпр.	баз.пер.	отч.пер.	баз.пер.	отч.пер.
1	72	70	6	7
2	84	90	5	4,8

Вычислить индекс средней себестоимости: а) переменного состава, б) постоянного состава, в) структурных сдвигов. Показать их взаимосвязь.

РЕШЕНИЕ:

а) Индекс средней себестоимости переменного состава равен

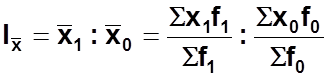
б) Индекс средней себестоимости постоянного состава равен

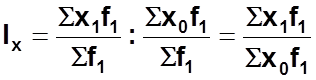
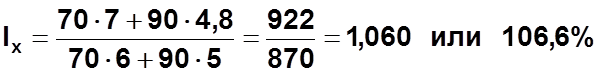
в) Индекс средней себестоимости структурных сдвигов равен:

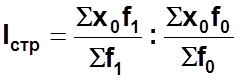
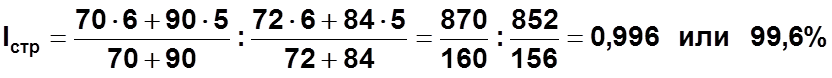
Взаимосвязь исчисленных индексов

1 2

Скачать файл