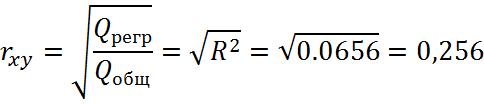

Вывод: связь практически отсутствует.
· Для парной степенной регрессии
Индекс парной корреляции:
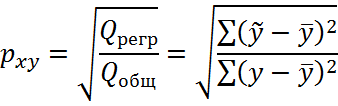
Регрессионные суммы составили:
![]()
![]()
Качество подбора линейных функций показывает индекс детерминации:
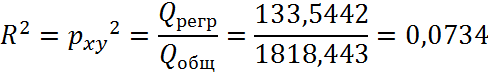
Следовательно, индекс парной корреляции составит:
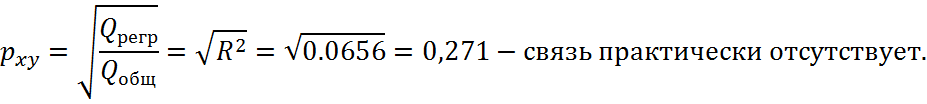
Вывод: 7,34% вариации результативного признака объясняется уравнением степенной регрессии. Доля необъясненной дисперсии в общей составляет 92,66%.
· Для парной экспоненциальной регрессии
Индекс парной корреляции:
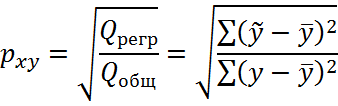
Регрессионные суммы составили:
![]()
![]()
Качество подбора линейных функций показывает индекс детерминации:
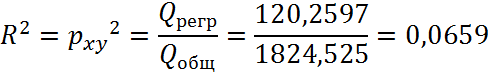
Следовательно, индекс парной корреляции составит:
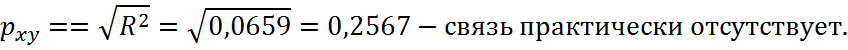
Вывод: 6,59% вариации результативного признака объясняется уравнением экспоненциальной регрессии. Доля необъясненной дисперсии в общей составляет 93,41%.
4) Сравнительную оценку силы связи фактора с результатом проведем с помощью среднего коэффициента эластичности. Он показывает, на сколько процентов в среднем по совокупности изменится результат y при изменении фактора x на 1% от своего среднего значения.
· Для парной линейной регрессии
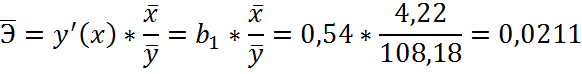
· Для парной степенной регрессии
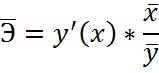
![]()
![]()
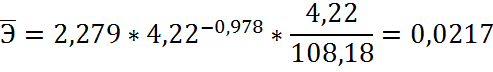
· Для парной экспоненциальной регрессии
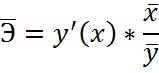
![]()
![]()
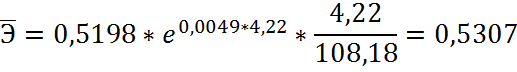
5) Оценку качества построенной модели покажет средняя ошибка аппроксимации – среднее отклонение расчетных значений от фактических.
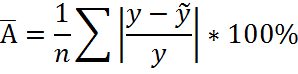
Допустимый
предел значений ![]() не более 8-10%.
не более 8-10%.
· Для парной линейной регрессии
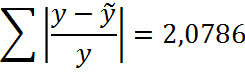
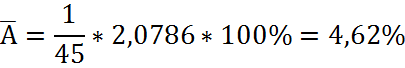
· Для парной степенной регрессии
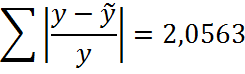
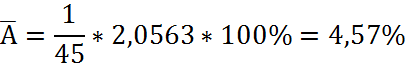
· Для парной экспоненциальной регрессии
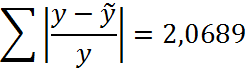
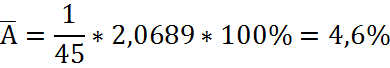
6) Значимость уравнения в целом оценивается по значению (величине) F – статистики Фишера. Для расчёта F используют дисперсии на одну степень свободы; такие дисперсии сравнимы между собой по величине, так как приведены к общей шкале.
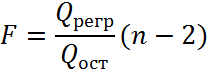
· Для парной линейной регрессии
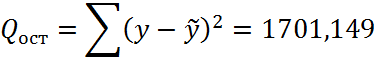
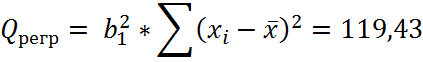
Таким образом, расчетное значение F – статистики Фишера составит:
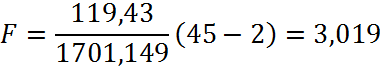
По таблице Фишера – Снедекора,
содержащей критические значения F
при разных уровнях γ существенности нулевой гипотезы и разных степенях
свободы df, найдём Fкр
(критическое значение) для данной задачи:![]()
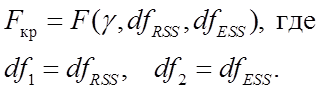
![]()
![]()
![]()
В данном случае расчётное значение F< Fкр, уравнение признается неадекватным.
· Для парной степенной регрессии
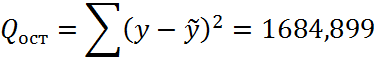
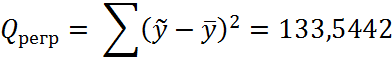
Таким образом, расчетное значение F – статистики Фишера составит:
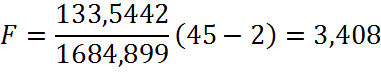
![]()
· Для парной экспоненциальной регрессии
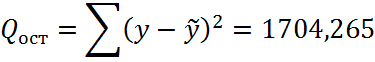
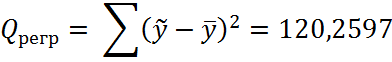
Таким образом, расчетное значение F – статистики Фишера составит:
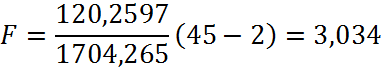
![]()
Вывод.
На основании рассчитанных в пп.4, 5, 6 показателей тесноты связи и качества уравнения можно сказать следующее:
ü наибольшее значение среднего коэффициента эластичности наблюдается в случае экспоненциального уравнения парной регрессии. Таким образом, связь фактора с результатом признается более тесной (Э > 0,5). При изменении фактора x на 1% от своего среднего значения результат y повысится на 0,53% в среднем по совокупности;
ü Значения средней ошибки аппроксимации для трех моделей находятся в пределах допустимых значений (от 8 до 10%). Отличаются незначительно, наибольшее значение для линейной регрессии (4,62%).
ü Во всех случаях расчётное значение F < Fкр, уравнение признается неадекватным. Наименьшее значение F-статистики для линейной модели (3,019). Набольшее значение F-статистики для степенной модели (3,41).
В целом можно признать наилучшим уравнение экспоненциальной парной регрессии:
![]()
7) При увеличении фактора на 5% от своего среднего уровня значение результата увеличится на 2,65% от своего среднего уровня.
![]()
![]()
Доверительный интервал
прогноза для уровня значимости ![]()
![]()
где ![]()
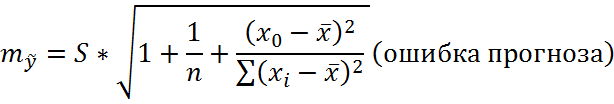
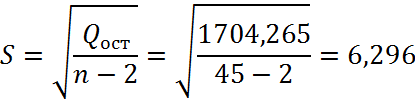
![]()
Следовательно, ошибка прогноза составит:
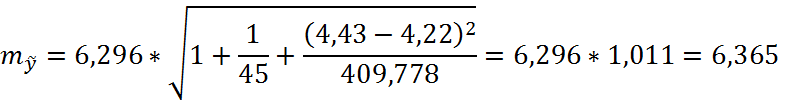
Нижняя граница доверительного интервала:
![]()
Верхняя граница доверительного интервала:
![]()
Доверительный интервал
прогноза для уровня значимости ![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.