Вариант 5.
1) Таблица исходных данных.
|
наблюдение |
ПК |
холодильники, морозильники |
|
1 |
1 |
103 |
|
2 |
2 |
99 |
|
3 |
2 |
105 |
|
4 |
2 |
102 |
|
5 |
1 |
106 |
|
6 |
6 |
106 |
|
7 |
1 |
100 |
|
8 |
3 |
100 |
|
9 |
2 |
113 |
|
10 |
14 |
106 |
|
11 |
6 |
111 |
|
12 |
3 |
106 |
|
13 |
6 |
115 |
|
14 |
1 |
108 |
|
15 |
4 |
102 |
|
16 |
5 |
102 |
|
17 |
4 |
110 |
|
18 |
9 |
106 |
|
19 |
5 |
111 |
|
20 |
8 |
103 |
|
21 |
3 |
104 |
|
22 |
7 |
105 |
|
23 |
3 |
102 |
|
24 |
8 |
107 |
|
25 |
4 |
96 |
|
26 |
3 |
99 |
|
27 |
4 |
109 |
|
28 |
2 |
104 |
|
29 |
5 |
116 |
|
30 |
1 |
106 |
|
31 |
8 |
109 |
|
32 |
4 |
116 |
|
33 |
1 |
108 |
|
34 |
1 |
109 |
|
35 |
5 |
119 |
|
36 |
4 |
111 |
|
37 |
1 |
105 |
|
38 |
2 |
120 |
|
39 |
3 |
114 |
|
40 |
6 |
119 |
|
41 |
2 |
109 |
|
42 |
6 |
113 |
|
43 |
14 |
121 |
|
44 |
4 |
124 |
|
45 |
4 |
109 |
В качестве результирующего признака выберем количество холодильников, в качестве фактора - кол-во компьютеров. Поле корреляции выглядит следующим образом:
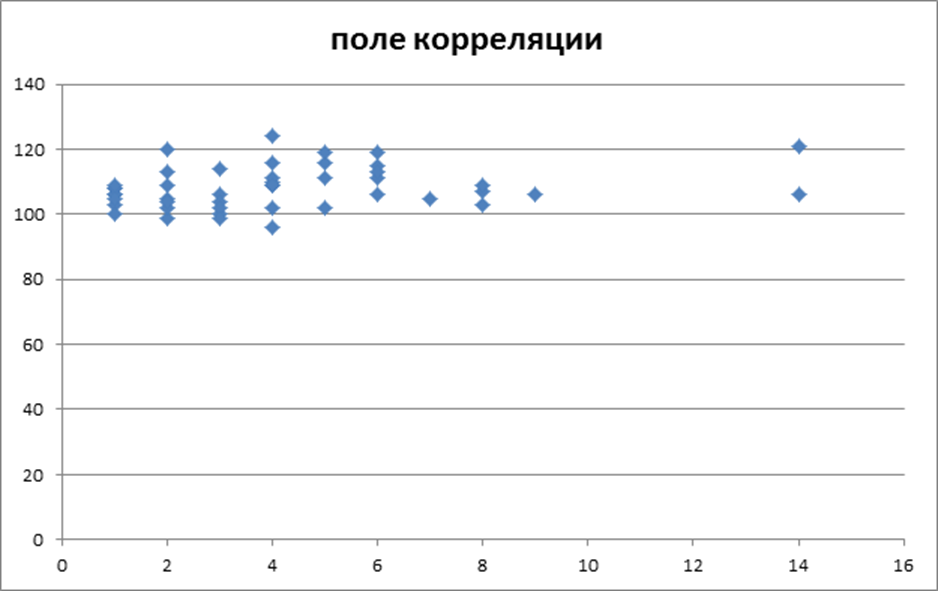
Предположительно форма связи между значениями результирующего признака и фактора нелинейная.
2) Построим различные модели парной регрессии и рассчитаем их параметры.
a) Рассчитаем параметры уравнения парной линейной регрессии.
Общий вид уравнения:
![]()
Отыскание
оценок параметров ![]() проводится с использованием классического
метода наименьших квадратов. Для этого составляется система нормальных
уравнений:
проводится с использованием классического
метода наименьших квадратов. Для этого составляется система нормальных
уравнений:
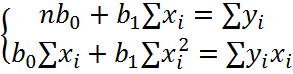
Решая систему уравнений методом Крамера, получим следующие значения оценок параметров:
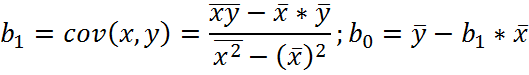
Расчет
парамеров парной линейной регрессии проведем в таблице 1. После этого подставим
в полученное уравнение регрессии эмпирические значения фактора и расчитаем прогнозные
(теоретические) значения результирующего признака (![]() . Также расситаем отклонения
эмпирических значений результирующего признака от теоретических (e).
. Также расситаем отклонения
эмпирических значений результирующего признака от теоретических (e).
Объем
выборки 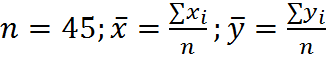
Таблица 1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.