Модели парной регрессии и расчет их параметров, страница 4

Рассчитаем параметры

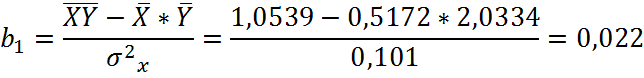
где

Получили линейное уравнение:

Выполнив его потенцирование, получим:

Подставляя в данное уравнение фактические значения x, получаем теоретические значения результата

№	x	y	yтеор	e
1	1	103	105,1962	-2,19619
2	2	99	106,7879	-7,78789
3	2	105	106,7879	-1,78789
4	2	102	106,7879	-4,78789
5	1	106	105,1962	0,803813
6	6	106	109,3602	-3,36017
7	1	100	105,1962	-5,19619
8	3	100	107,7301	-7,73012
9	2	113	106,7879	6,212107
10	14	106	111,3863	-5,38626
11	6	111	109,3602	1,639832
12	3	106	107,7301	-1,73012
13	6	115	109,3602	5,639832
14	1	108	105,1962	2,803813
15	4	102	108,4037	-6,40368
16	5	102	108,929	-6,92903
17	4	110	108,4037	1,596318
18	9	106	110,3251	-4,32509
19	5	111	108,929	2,070965
20	8	103	110,0439	-7,04392
21	3	104	107,7301	-3,73012
22	7	105	109,726	-4,72602
23	3	102	107,7301	-5,73012
24	8	107	110,0439	-3,04392
25	4	96	108,4037	-12,4037
26	3	99	107,7301	-8,73012
27	4	109	108,4037	0,596318
28	2	104	106,7879	-2,78789
29	5	116	108,929	7,070965
30	1	106	105,1962	0,803813
31	8	109	110,0439	-1,04392
32	4	116	108,4037	7,596318
33	1	108	105,1962	2,803813
34	1	109	105,1962	3,803813
35	5	119	108,929	10,07097
36	4	111	108,4037	2,596318
37	1	105	105,1962	-0,19619
38	2	120	106,7879	13,21211
39	3	114	107,7301	6,269878
40	6	119	109,3602	9,639832
41	2	109	106,7879	2,212107
42	6	113	109,3602	3,639832
43	14	121	111,3863	9,613737
44	4	124	108,4037	15,59632
45	4	109	108,4037	0,596318
Ср.знач.	4,2222	108,1778

c) Построению экспоненциальной модели предшествует процедура линеаризации переменных. Линеаризация производится путем логарифмирования обеих частей уравнения:

Отыскание оценок параметров проводится с использованием классического метода наименьших квадратов.

Для расчетов используем таблицу 3.

Таблица 3.

1 2 3 4 5 6 7

Скачать файл