Рассчитаем
параметры ![]()
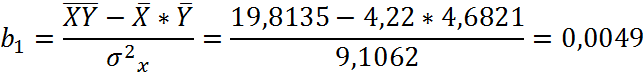
где
![]()
![]()
Получили линейное
уравнение: ![]()
Выполнив его потенцирование, получим:
![]()
Подставляя
в данное уравнение фактические значения x,
получаем теоретические значения результата ![]()
|
№ |
x |
y |
yтеор |
e |
|
1 |
1 |
103 |
106,2452 |
-3,2452 |
|
2 |
2 |
99 |
106,7688 |
-7,76877 |
|
3 |
2 |
105 |
106,7688 |
-1,76877 |
|
4 |
2 |
102 |
106,7688 |
-4,76877 |
|
5 |
1 |
106 |
106,2452 |
-0,2452 |
|
6 |
6 |
106 |
108,889 |
-2,88898 |
|
7 |
1 |
100 |
106,2452 |
-6,2452 |
|
8 |
3 |
100 |
107,2949 |
-7,29492 |
|
9 |
2 |
113 |
106,7688 |
6,231233 |
|
10 |
14 |
106 |
113,2565 |
-7,25654 |
|
11 |
6 |
111 |
108,889 |
2,111025 |
|
12 |
3 |
106 |
107,2949 |
-1,29492 |
|
13 |
6 |
115 |
108,889 |
6,111025 |
|
14 |
1 |
108 |
106,2452 |
1,754803 |
|
15 |
4 |
102 |
107,8237 |
-5,82366 |
|
16 |
5 |
102 |
108,355 |
-6,35501 |
|
17 |
4 |
110 |
107,8237 |
2,17634 |
|
18 |
9 |
106 |
110,5067 |
-4,50672 |
|
19 |
5 |
111 |
108,355 |
2,644992 |
|
20 |
8 |
103 |
109,9648 |
-6,96482 |
|
21 |
3 |
104 |
107,2949 |
-3,29492 |
|
22 |
7 |
105 |
109,4256 |
-4,42557 |
|
23 |
3 |
102 |
107,2949 |
-5,29492 |
|
24 |
8 |
107 |
109,9648 |
-2,96482 |
|
25 |
4 |
96 |
107,8237 |
-11,8237 |
|
26 |
3 |
99 |
107,2949 |
-8,29492 |
|
27 |
4 |
109 |
107,8237 |
1,17634 |
|
28 |
2 |
104 |
106,7688 |
-2,76877 |
|
29 |
5 |
116 |
108,355 |
7,644992 |
|
30 |
1 |
106 |
106,2452 |
-0,2452 |
|
31 |
8 |
109 |
109,9648 |
-0,96482 |
|
32 |
4 |
116 |
107,8237 |
8,17634 |
|
33 |
1 |
108 |
106,2452 |
1,754803 |
|
34 |
1 |
109 |
106,2452 |
2,754803 |
|
35 |
5 |
119 |
108,355 |
10,64499 |
|
36 |
4 |
111 |
107,8237 |
3,17634 |
|
37 |
1 |
105 |
106,2452 |
-1,2452 |
|
38 |
2 |
120 |
106,7688 |
13,23123 |
|
39 |
3 |
114 |
107,2949 |
6,705083 |
|
40 |
6 |
119 |
108,889 |
10,11102 |
|
41 |
2 |
109 |
106,7688 |
2,231233 |
|
42 |
6 |
113 |
108,889 |
4,111025 |
|
43 |
14 |
121 |
113,2565 |
7,743462 |
|
44 |
4 |
124 |
107,8237 |
16,17634 |
|
45 |
4 |
109 |
107,8237 |
1,17634 |
3) Показатели тесноты связи
· Для парной линейной регрессии
Линейный коэффициент парной корреляции
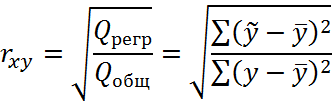
или
![]()
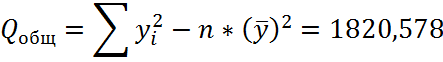
Качество подбора линейных функций показывает коэффициент детерминации:
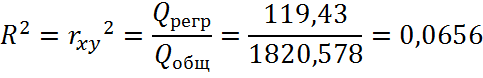
Вывод: 6,56% вариации результативного признака объясняется уравнением линейной регрессии. Доля необъясненной дисперсии в общей составляет 93,44%.
Следовательно, коэффициент парной корреляции составит:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.