Метод координат. Векторная алгебра. Скалярное умножение. Плоскость в пространстве. Прямая в пространстве

Метод координат.

Основан на применении систем координат как на плоскости, так и в пространстве.

Говорят, что, например, на плоскости введена некоторая система координат, если указан способ, позволяющий характеризовать положение произвольной точки на плоскости некоторым набором чисел, называемых координатами этой точки.

При выводе уравнений кривых часто используются формулы расстояния между двумя точками:  и деления отрезка в заданном отношении: 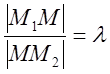 (можно показать, что: ).

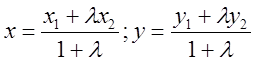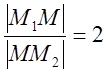Пусть на плоскости даны точки  и , для которых . Для определения типа кривой необходимо получить её уравнение. Для этого сначала введём на плоскости декартову систему координат так, что бы точки располагались на оси абсцисс симметрично относительно начала координат. Введём произвольную точку , удовлетворяющую указанному условию. Выразим длины через координаты: . Таким образом, уравнение: 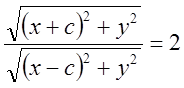. Упростим: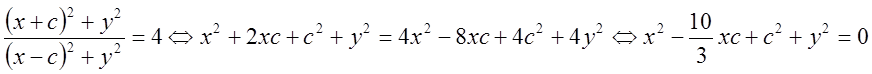 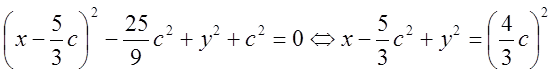 - окружность.

Векторная алгебра.

Вектор (как на плоскости, так и в пространстве) – это всякий направленный отрезок.

Если даны координаты начальной  и концевой  точек, то длина вектора:

Линейные операции над векторами:

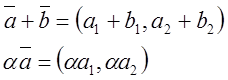
Скалярное умножение.

, где  - угол между векторами.

Свойства:

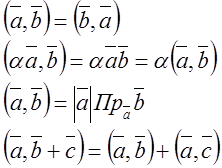
Прямая на плоскости.

Известно, что всякая прямая на плоскости, не являющаяся вертикалью, задаётся уравнением , а вертикальная прямая задаётся уравнением вида . Следовательно, общее уравнение:

.

Всякая прямая на плоскости задаётся этим уравнением, и наоборот, любое такое уравнение, для которого хотя бы один из коэффициентов отличен от нуля, задаёт некоторую прямую.

Замечание. Всякое уравнение задаёт единственную прямую. Напротив, одну прямую можно задать различными уравнениями. Таким образом, уравнение кривой определяется с точностью до пропорциональности.

Построение уравнений прямых.

Всякий вектор, перпендикулярный данной прямой, называется нормалью:  - нормаль для .

Действительно, взяв 2 точки  и , лежащие на данной прямой, получим уравнения:  и  соответственно. Вычитая, получим: . Но вектор  лежит на прямой, а  означает, что скалярное произведение этого вектора на  равно нулю. Следовательно, вектора ортогональны (перпендикулярны), и  - нормаль.

Пусть известны  на прямой  и нормаль . Такая прямая имеет уравнение: .

Пусть прямая задана точкой  и направляющим вектором . Направляющим для данной прямой называют всякий ненулевой вектор, лежащий на коллинеарной этой прямой. Тогда: .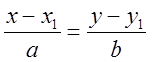

Уравнение прямой, проходящей через 2 заданные точки: .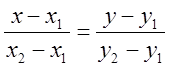

Пусть прямая пересекает оси  и  в точках  и  соответственно. Тогда прямая задаётся уравнением: .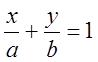

Решение важнейших задач.

1. Пусть заданы 2 прямые  и . Угол между прямыми сводится к нахождению угла между нормалями к этим прямым: .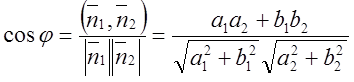

Замечание. Если , то измерен острый угол.

В частности, условие  равносильно перпендикулярности прямых. Условие их коллинеарности можно записать в виде: 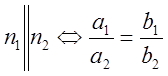. В этом случае прямые либо параллельны (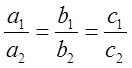) либо совпадают ().

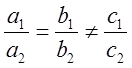2. Расстояние от точки  до прямой : .

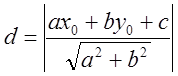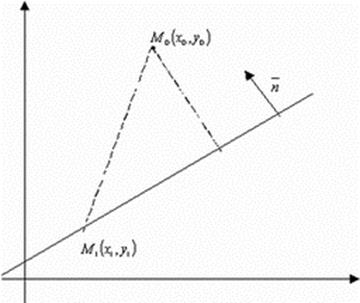
Выберем вспомогательную точку . Тогда расстояние – есть абсолютная величина проекции вектора  на вектор  прямой. Тогда: 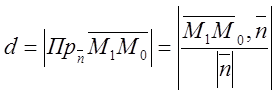, и т.к.  и , то подставляя, получаем указанную выше формулу.

Замечание. Деление уравнения   на  называется нормированием уравнения.

Плоскость в пространстве.

Нормалью к плоскости является вектор .

Уравнение плоскости, проходящей через точку  и имеющей нормаль : .

Уравнение плоскости в отрезках: если оси  пересекаются в точках  соответственно, то уравнение: .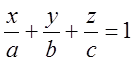

Угол между плоскостями: .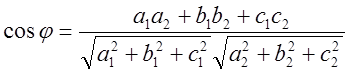

Плоскости совпадают если 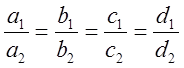 и параллельны если .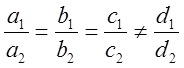

Векторное произведение.

В отличие от скалярного, векторное произведение  является вектором.

Векторы  образуют т.н. «правую дробь». Т.е. если большой палец правой руки расположить вдоль , указательный – вдоль , то безымянный палец естественным образом укажет направление .

Смешанное произведение.

Пусть даны 3 вектора . Рассмотрим задачу по вычислению объёма параллелепипеда, построенного на этих векторах.

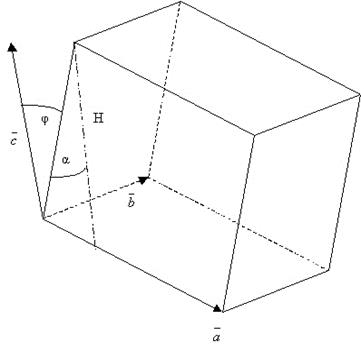
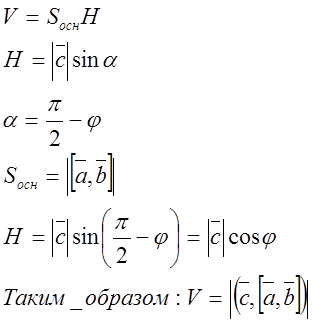
Иначе, формулу можно объяснить:

Имеем , где H – высота. , а . Но эта нормаль служит направлением для векторного произведения , значит φ – угол между  и . Следовательно, искомый объём – есть абсолютная величина скалярного произведения  и .

Смешанным произведением векторов  называют скалярную величину .

Иначе формула может быть выведена через координаты перемножаемых векторов.