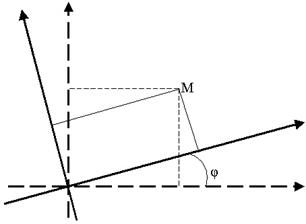
Пусть M – произвольная точка на плоскости, (x,y) –
её старые координаты, ![]() -новые. Тогда:
-новые. Тогда:
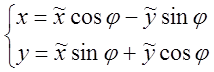
Для произвольного уравнения 2-го порядка можно подобрать такой угол, что произведение координат в уравнении станут нулём. В таком случае квадратичные слагаемые преобразуются и по их характеру можно определить тип кривой:
![]() :
: ![]() ;
;
![]() ;
;
Пусть после поворота получено уравнение: ![]() . Выделяя полные квадраты (параллельный
перенос), можно избавиться от линейных членов и прийти окончательно к уравнению
. Выделяя полные квадраты (параллельный
перенос), можно избавиться от линейных членов и прийти окончательно к уравнению
![]() . Тогда типы кривых:
. Тогда типы кривых:
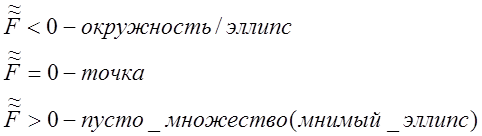
Если же ![]() , то:
, то:
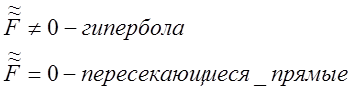
Если ![]() , то уравнение задаётся
с помощью подходящего переноса и:
, то уравнение задаётся
с помощью подходящего переноса и:

Поверхности 2-го порядка и их исследование.
Это поверхности, задающиеся в декартовых координат уравнениями 2-ой степени.
1. Сфера.
![]()
a,b,c – координаты центра, r – радиус.
2. Эллипсоид.

3. Гиперболоид.
Однополостной: 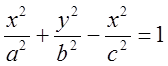 Двуполостной:
Двуполостной:
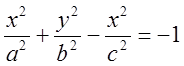
4. Параболоид:
Эллиптический: 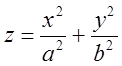 Гиперболический:
Гиперболический:
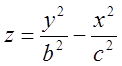
5. Цилиндрические поверхности.
Это поверхности обязательно 2-го порядка, которые наряду с каждой своей точкой содержат всю прямую, проходящую через эту точку и параллельную некоторому фиксированному для данной прямой направлению.
Всякая такая прямая называется образующей для данной поверхности.
Пусть образующая параллельна Oz. Тогда уравнение такой поверхности имеет вид Г(x,y)=0. Координата Z не входит в уравнение. Действительно, если M0(x0,y0,z0) лежит на такой поверхности, то и всякая точка M’(x0,y0,z’) лежит на этой поверхности, т.е. вся вертикальная прямая, проходящая через M0 лежит на поверхности.
Если Г(x,y)=0 – произвольное уравнение 2-го порядка, то оно определяет в 3-мерном пространстве цилиндр, образующая которого параллельна оси OZ. Например, x2+y2=r2 – прямой круговой цилиндр.
Для исследования поверхностей используется метод сечений, исследующий кривые, получающиеся сечением данной поверхности плоскостями, параллельными плоскостями.
Рассмотрим уравнение однополостного гиперболоида: 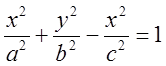 .
.
Сечение z=h: 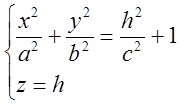 - определяет эллипсы,
с тем большими полуосями, чем больше |h|.
- определяет эллипсы,
с тем большими полуосями, чем больше |h|.
Сечение x=h: 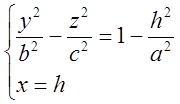 - пересекающиеся
прямые в случае h2=a2 и гипербола, соединяющая вершины эллипса, в случае h2≠a2.
- пересекающиеся
прямые в случае h2=a2 и гипербола, соединяющая вершины эллипса, в случае h2≠a2.
Сечение y=h: 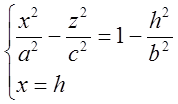 - гипербола.
- гипербола.
Комплексные числа.
Это объект вида a+ib, где a и b – действительные числа, а i – мнимая единица. Сложение и умножение комплексных чисел определяется формулами:
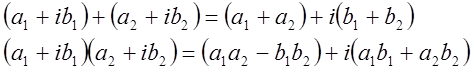
Обычно комплексное число обозначают как Z, а множество всех комплексных чисел – C.
z2=zz.
Пусть теперь z=0+i1. тогда:
i2=(0+i)(o+i)=-1+0i=-1
i2=-1.
Имея ввиду последнее равенство i2 всегда можно заменять на –1.
Деление комплексных чисел:
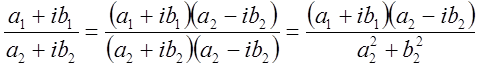
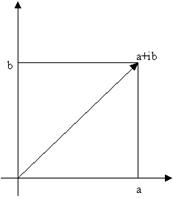
Геометрически комплексные числа интерпретируются как векторы на плоскости, но при этом OX - действительная ось, OY – мнимая.
Для z=a+ib действительное a – есть действительная часть (ReZ), b – мнимая часть (ImZ).
Сложение и умножение комплексных чисел соответствует сложению двумерных векторов.
Комплексные числа имеют иную, тригонометрическую форму.
Пусть |z| - длина соответствующего вектора, тогда ![]() . Аргумент комплексного числа z≠0 –
угол, образуемый этим вектором с положительным лучом оси OX.
. Аргумент комплексного числа z≠0 –
угол, образуемый этим вектором с положительным лучом оси OX.
Замечание. Для z≠0 его аргумент определён неоднозначно. Считается, что угол – один из его аргументов.
Для ![]() и z≠0:
и z≠0:
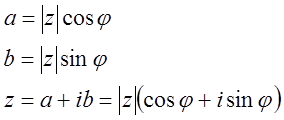
Последнее выражение называется тригонометрической формой комплексного числа.
Умножение в тригонометрической форме:
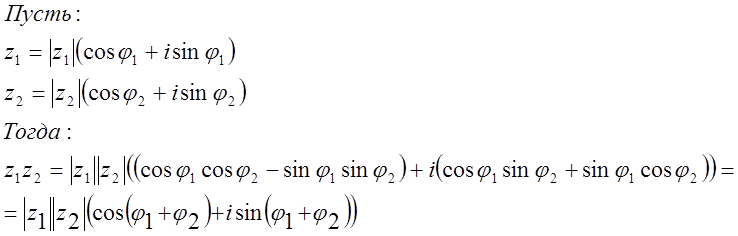
Т.е. модули перемножаются, а аргументы складываются. Из этой формулы следует формула Муавра:
![]()
Так же можно вывести формулы Эйлера:
По определению, ![]() . С
помощью этого определения тригонометрическая форма комплексного числа
преобразуется в т.н. показательную:
. С
помощью этого определения тригонометрическая форма комплексного числа
преобразуется в т.н. показательную: ![]() . С другой стороны,
. С другой стороны, 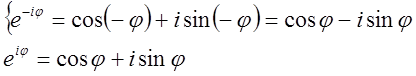 , отсюда можно получить формулы Эйлера:
, отсюда можно получить формулы Эйлера:
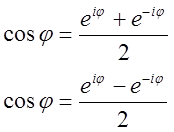
Комплексные числа облегчают вычисление различных неопределённых интегралов; формулы преобразования координат при повороте системы можно получить, основываясь на комплексной интерпретации поворота; можно получить ряд тригонометрических формул:
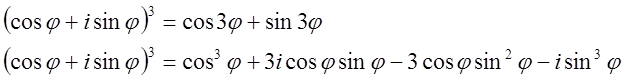
Можно привести формулу извлечения корней n-степени
из произвольного комплексного числа z≠0, n![]() Z, n≥2:
Z, n≥2: ![]() . Для всякого
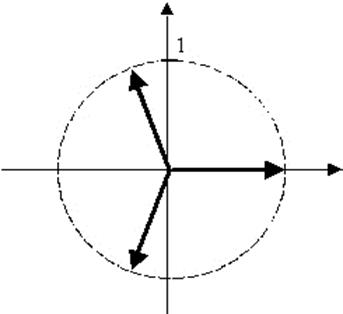
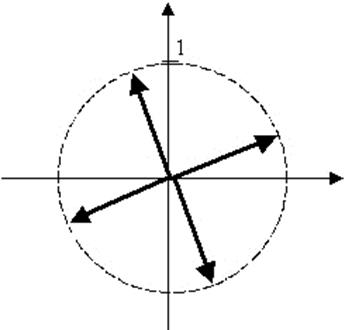
комплексного z≠0 и всякого натурального n≥2 существует ровно n
корней n-ой степени из z и их значения
даются формулой:
. Для всякого
комплексного z≠0 и всякого натурального n≥2 существует ровно n
корней n-ой степени из z и их значения
даются формулой:
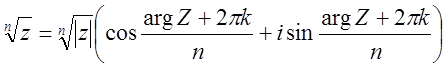
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.