Расчет электрических фильтров, страница 5

Определим порядок фильтра n по формуле 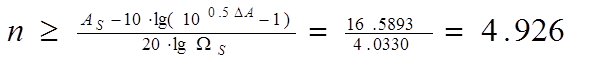(2.4):

                      (2.4)

Берем ближайшее целое в качестве порядка ФПНЧ n = 5. Схема фильтра 5-го порядка представлена на рис. 2.1.

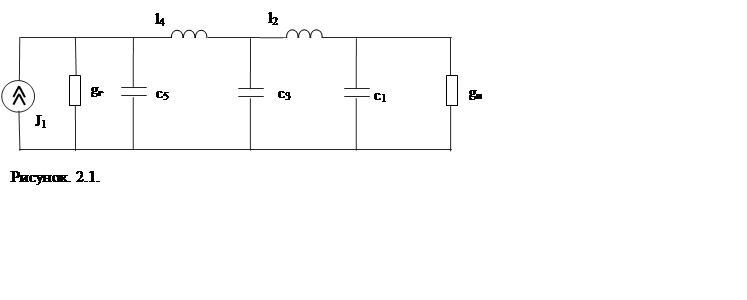
Согласно таблице 10 [4] для dA = 1 и  n = 5 нормированные элементы ФПНЧ имеют значения :

c₁  =  l’₁ = 0.618 = c₅= l’₅; l₂ = c’₂ = 1.618 = l₄ = c’₄; c₃ = l’₃ = 2.

От схемы на рисунке 2.1 перейдем к схеме полосового фильтра, нормированные элементы которого найдем по формулам :

                        c’_1п = c’ _5п = k · c’₁                                         (2.5 )

                                              1

                        l’_1п = l’_5п =  ¾¾¾                                        ( 2.6 )

                                            k · c’ ₁    

                        c’_3п = k · c’₃                                                    (2.7 )

                                       1

                        l’_3п =   ¾¾¾                                                ( 2.8 )

                                    k · c’₃

                        l’_2п = l’_4п = k · l’₂                                            ( 2.9 )

                                                 1        

                        c'_2п = c’_4п = ¾¾¾                                        ( 2.10 )

                                             k · l’₂     

Схема ПФ изображена на рисунке 2.2.

 

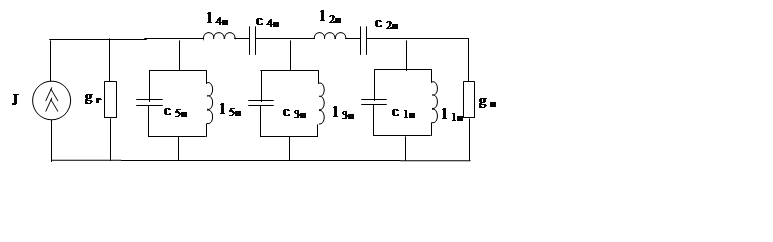Рисунок 2.2. Схема полосового фильтра

В результате расчета получили следующие значения:

с_1п = 1.685  = с_5п = l’_1п = l’_5п

l_1п = 0.5933 = l’_5п

c _2п = 0.2266 = с _4п =  l’ _2п = l’ _4п

l _2п = 4.4127 = l _4п = с’ _2п = с’ _4п

с _3п = 5.4545 = l’ _3п

l’ _3п  = 0.1833 = c’ _3п­­ .

Перейдем к денормированным значениям по формулам (2.12 ):

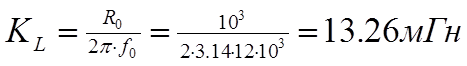
                                                                                                                           (2.12)

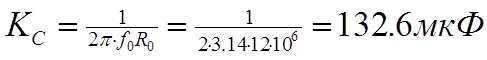
Теперь по формулам (2.13) – (2.18) вычислим номинальные значения индуктивностей и емкостей полосового фильтра:

                                              (2.13)

                                           (2.14)

                                          (2.15)

                                          (2.16)

                                                     (2.17)

                                                     (2.18)

Рассчитаем ослабление ПФ по формуле (2.19):

                                                              (2.19)

Предварительно найдем нормированные частоты по формуле (2.2). Получим:

W _f0  = 0 ;

W _f1 = 1;

W _f-1 = -1 ;

W _fs2 = 1.591;

W _{1.5 fs2} = 4.09;

W _2fs2 = 6.249;

В результате расчета по формуле (2.19) получили следующие значения:

 A _f0 =0 ;

 A _f1 = 1 дБ;

А _f-1 = 1 дБ;

A _fS2 = 14.457 дБ;

A _{1.5 fs2} = 55.304

A _{2 fS2} = 73.71

Зависимость ослабления от частоты представлена на рисунке 2.3.

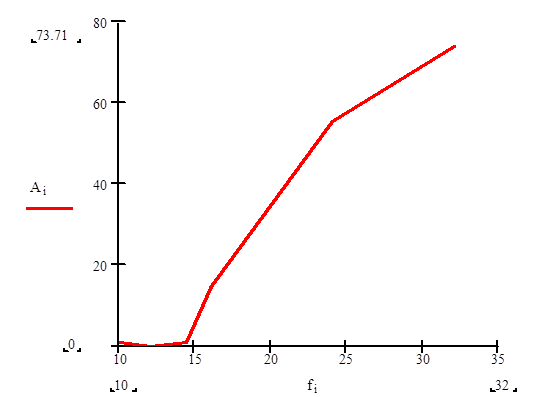
Рис . 2 . 3 . График функции ослабления  ПФ от частоты .

СПИСОК ЛИТЕРАТУРЫ

1.В.П.Бакалов , А.Н. Игнатов , Б.И. Крук .Основы теории электрических цепей и электроники : Учебник для вузов М.: Радио и связь,1989

2.Шебес М.Р., Каблукова М.В. Задачник по теории линейных электрических цепей. Учебное пособие для электротехнических, радиотехнических специальностей вузов.-4-е изд. перераб. и доп.- М.: Высшая школа ,1990

3.В.П.Бакалов , В.М. Рожков .Теория электрических цепей .Методические указания и контрольные задания №3 и №4.-Новосибирск :СибГУТИ,1999

4.Шебес М.Р., Знаменский А.Е. Задания на курсовую работу и методические указания к ним по курсу  ² Теория электрических цепей ²  по теме  ² Расчет электрических фильтров ².-М.:МИС. Кафедра теории электрических цепей,1991