в) делим второй делитель на второй остаток :
|
2 * S 3 + 3.236068 * S 2 + 2.618034 * S + 1 |
S 2 + 1.618034 * S + 1 |
|
- (2 * S 3 + 3.236068 * S 2 + 2 * S) |
|
|
0.618034 * S + 1 |
2 * S ® l ‘ 3 |
г) делим третий делитель на третий остаток :
|
S 2 + 1.618034 * S + 1 |
0.618034 * S + 1 |
|
- (S 2 + 1.618034 * S) |
|
|
1 |
1.618034 * S ® c’ 2 |
д) четвертый делитель делим на четвертый остаток:
|
0.618034 * S + 1 |
1 |
|
- (0.618034 * S) |
|
|
1 |
0.618034 * S ® l’ 1 |
е) делим пятый делитель на пятый остаток :
|
1 |
1 |
|
-1 |
|
|
0 |
1® r’ Н |
Получена схема на рисунке 1.1 .По расчетным данным начертим график зависимости ослабления от частоты .
|
Частота, кГц |
Ослабление, ΔА, дБ |
|
f1, 1 |
0.5 |
|
f0, 1.23 |
3 |
|
1.5 f1, |
9.05 |
|
fs, 1.75 |
15.3 |
|
2 f1 |
21 |
Рис. 1. 3. График зависимости ослабления ФНЧ Баттерворта от частоты.

Задача 1, б.
Рассчитать двусторонне нагруженный ФНЧ Чебышева по данным: в полосе пропускания при 1 кГц > f > 0 ослабление не должно превышать 0.5 дБ, а при частотах 1.75 кГц и больших оно должно быть не менее АS. Сопротивления генератора и нагрузки одинаковы Rг = Rн = 1 кОм.
Рассчитать:
а) порядок фильтра n;
б) по таблице 10 [4] и аналитически найти нормированные элементы ФНЧ;
в) начертить схему фильтра;
г) вычислить номинальные (истинные) значения элементов ФНЧ;
д) рассчитать ослабление при частотах f1, fS, 1.5 fS, 2fS;
е) начертить график зависимости ослабления от частоты.
Решение:
Найдем порядок фильтра по формуле (1.1):
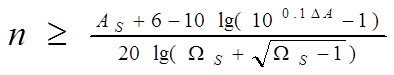 (1.1)
(1.1)
Для этого определим нормированную частоту по формуле (1.2):
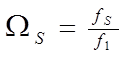 (1.2)
(1.2)
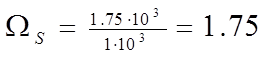

Округляем результат до ближайшего целого. Получаем n = 3 (ФНЧ 3-го порядка).
Вычисляем вспомогательные величины:
![]() (1.3)
(1.3)
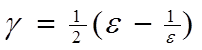 ,
, 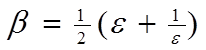 (1.4)
(1.4)
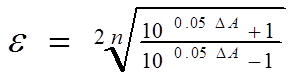 (1.5)
(1.5)

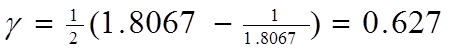
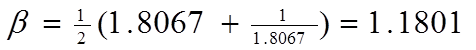
Вычисляем нормированные значения полюсов по формуле (1.3):
При n = 3, k = 1:
S1 = -0.313 + 1.022 i;
При n = 3, k = 3:
S3 = -0.313 – 1.022 i;
При n = 3, k = 2:
S2 = -0.626
Вычислим произведение двух сопряженных комплексов:
(S – S1)·(S – S3) = (S + 0.313 – 1.022i) · (S + 0.313 + 1.022i) =
= S2 +0.313S – 1.022S·i +0.313S + 0.09797 – 0.31989·i + 1.022S·i +0.31989·i +1.0445 =
S2 + 0.627S + 1.143.
Определим полином Гурвица (знаменатель передаточной функции):
US(S) = (S – S1)(S – S3)(S – S2) = (S2 + 0.627S + 1.143) ·(S + 0.627) =
= S3 + 0.627S2 +1.143S + 0.627S2 + 0.393S + 0.717 = S3 + 1.254S2 +1.536S + 0.717
В соответствии с таблицей 4 [4] функция фильтрации
h(S) = S3 + 0.75S
Входное сопротивление, если взять верхние знаки, определяется формулой (1.4):
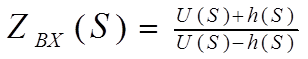 (1.4)
(1.4)
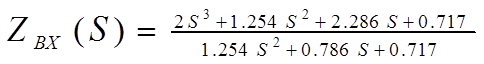
Разложим это выражение в цепную дробь:
а) делим числитель на знаменатель:
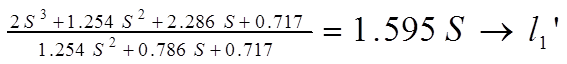 , первый остаток 1.143S+0.717;
, первый остаток 1.143S+0.717;
б) делим делитель на 1-й остаток:
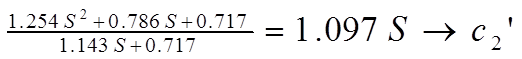 , второй остаток 0.717;
, второй остаток 0.717;
в) делим 2-1 делитель на 2-1 остаток:
 , третий остаток 0.717;
, третий остаток 0.717;
г) делим 3-1 делитель на 3-1 остаток:
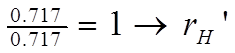
Получена следующая цепная дробь:
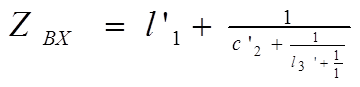
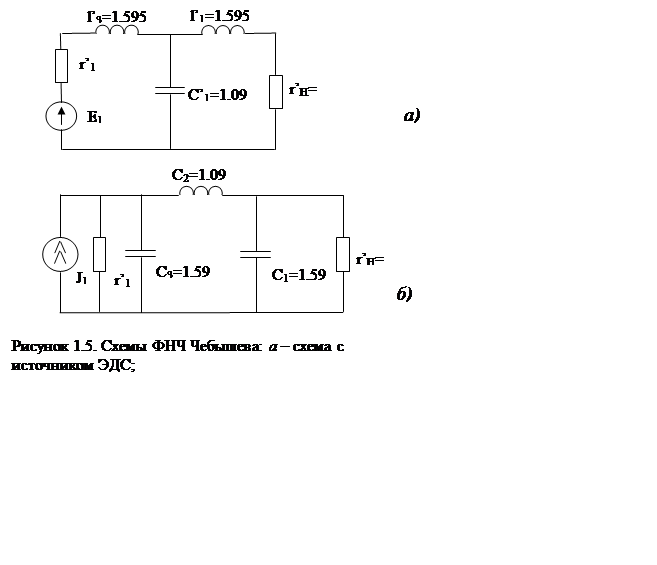
Ей соответствует схема на рис. 1.5, а.
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.