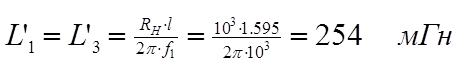 (1.5)
(1.5)
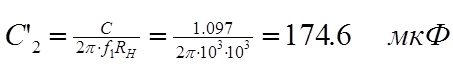 (1.6)
(1.6)
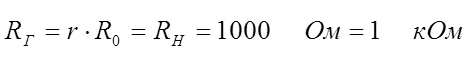 (1.7)
(1.7)
Соответствующие схемы приведены на рис. 1.5, только вместо нормированных значений элементов будут стоять истинные номинальные значения.
Рассчитаем ослабления на заданных частотах по формуле (1.8):
![]() (1.8)
(1.8)
Формула записана с учетом того, что ареа-косинус определяется как
![]()
Определим нормированные частоты Ω для частот f1, fS, 1.5fS, 2fS:
Ω f1 = f1/f1 =1;
Ω fs = fS/f1 = 1.75·103/1·103 = 1.75;
Ω 1.5fs = 1.5fS/f1 = 1.5·1.75·103/1·103 = 2.625;
Ω 2fs = 2fS/f1 = 2·1.75·103/1·103 = 3.5;
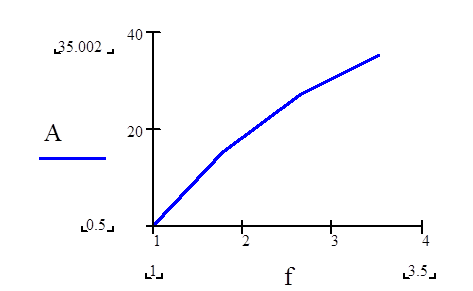
Результат расчета ослабления по формуле (1.8):
A f1 = 0.5;
A fs = 15.182;
A 1.5fs = 27.061;
A 2fs = 35.002;
Кривая зависимости ослабления от частоты изображена на рис. 1.6.
|
При расчете фильтра с помощью таблицы определим порядок фильтра по формуле (1.1). Получим n = 3. Согласно таблице 10 [4] нормированные элементы ФНЧ Чебышева 3-го порядка при ослаблении ΔА = 0.5 дБ равны с1 = l’1 = 1.596, l2 = c’2 = 1.097, c3 = l’3 = 1.596. При разложении выражения для входного сопротивления в цепную дробь получили те же значения, что и в таблице, следовательно, аналитический расчет выполнен правильно и при расчете при помощи таблицы мы получим те же значения.
Рассчитать симметричный ПФ Баттерворта или Чебышева, нагруженный двусторонне по следующим данным: нижняя граница полосы пропускания f -1 = 10 кГц ; средняя геометрическая частота f 1 = 14.4 кГц; ослабление в полосе пропускания должно быть не более dA =1 дБ, а при частоте f S2 = 16 кГц ослабление должно быть не менее A S2 = 14 дБ ; сопротивление нагрузки фильтра R Г = R Н = R = 1 кОм.
Рассчитать:
а) порядок фильтра n;
б) нормированные элементы НЧ прототипа (таблицы 9 [4] и 10 [4]);
в) с помощью частотного преобразования найти элементы ПФ;
г) начертить схему;
д) найти истинные значения элементов фильтра;
е) рассчитать ослабление на частотах: f 0, f -1 , f 1 , f S2 , 1.5* f S2 , 2* f S2 ;
ж) начертить кривую ослабления в зависимости от частоты.
Решение:
Рассчитаем симметричный ПФ Баттерворта. Найдем верхнюю границу полосы пропускания из формулы
f 0 = Ö (f -1 * f 1 ) (2.1)
f 0 = (f1·f-1)0.5 = (10 · 103·14.4·103)0.5 = 12 кГц.
Определим среднюю геометрическую частоту низкочастотного прототипа W S по формулам:
f S2 f 0
W S = k · (¾¾¾¾ - ¾¾¾ ) (2.2 )
f 0 f S2
f 0
k = ¾¾¾¾¾¾¾ (2.3)
f 1 - f -1
12 · 10 3 16 · 10 3 12 · 10 3
W S = ¾¾¾¾¾¾¾ · ( ¾¾¾¾¾ - ¾¾¾¾¾ ) = 1.591
(14.4 - 10 ) ·10 3 12 · 10 3 16 · 10 3
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.