Другие предметы \ Основы передачи дискретных сообщений

Расчет скорости передачи информации и вероятности ошибочного приема символов сообщений системой передачи дискретных сообщений, страница 6

 Рисунок 2.1 Схема кодера при tи = 1.

 Проверим правильность построения схемы кодера путем прогона информационных разрядов через схему кодера, проверочные разряды должны появиться на 7-ом такте.

  Таблица 2.1.

№ такта

вход

Х0

Х1

Х2

Х3

Исх.сост.

0

0

0

0

1

0

1

1

0

0

2

1

0

1

1

0

3

1

1

1

1

1

4

1

0

1

1

1

5

1

0

0

1

1

6

0

0

0

0

1

7

1

1

1

0

0

 Пусть tи = 2.

 Сделаем расчет для tи = 2 аналогично как при tи = 1.

 Вычислим вероятность неправильногоприема символа при условии исправления двукратной ошибки.

 

 ,                                                   

где k– число информационных разрядов, в нашем случае k = 7,

      tи – кратность исправляемых  кодомошибок, tи = 2.

.

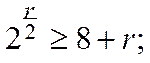
Скорость передачи данных определим по формуле [16]:

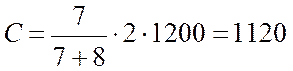 Бит/с.                               

 Образующий полином найдем пользуясь таблицей 2 [1]:

 r/tи = 8/2 = 4 (4-й столбец).

Минимальное кодовое расстояние равно:

,

i = 5 – 2 = 3.

Рх = (х4 + х + 1)(х4 + х3 +х2 + х + 1) = х8 + х7 + х6 + х4 + 1.

Рх = 111010001- образующее число.

 Пусть число информационных разрядов К = 1011110. Разделим по модулю 2 это число на образующее число, приписав, справа к информационным разрядам 00000000, так как число проверочных разрядов r = 8.

          1011110 00000000    111010001

          111010001                  1111010

            101010010

            111010001

              100000110

              111010001

                 110101110

                 111010001

                    0111111100

                       111010001

                         001011010 - остаток (проверочные разряды).

 Дополним информационные разряды проверочными и проверим делимость полученной кодовой комбинации на проверочное число.

           101111001011010   111010001

           111010001                   1111010

            101010000

            111010001

              100000011

              111010001

                110100101

                111010001

                  0111010001

                     111010001

            00000000   - остаток нулевой


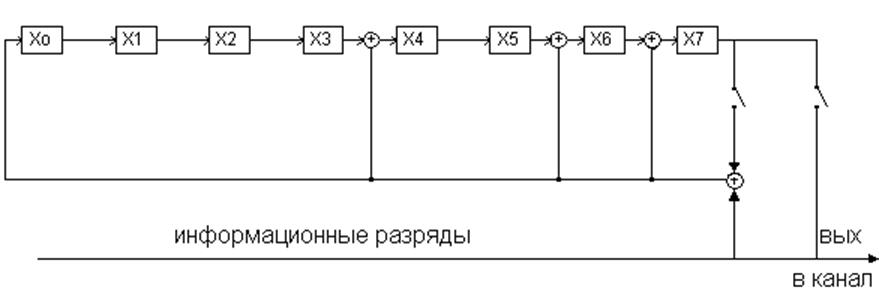Построим схему кодера циклического кода.

Рисунок 2.2 Схема кодера при tи = 2.

 Проверим правильность построения схемы кодера путем прогона информационных разрядов через схему кодера, проверочные разряды должны появиться на 7-ом такте.

  Таблица 2.2.

№ такта

вход

Х0

Х1

Х2

Х3

Х4

Х5

Х6

Х7

Исх.сост.

0

0

0

0

0

0

0

0

1

1

1

0

0

0

1

0

1

1

2

0

1

1

0

0

1

1

1

0

3

1

1

1

1

0

1

1

0

0

4

1

1

1

1

1

1

1

0

1

5

1

0

1

1

1

1

1

1

0

6

1

1

0

1

1

0

1

0

0

7

0

0

1

0

1

1

0

1

0

 Пусть tи = 3.

 Вычислим вероятность неправильногоприема символа при условии исправления трехкратной ошибки.

Скачать файл