избыточность, все символы появляются равновероятно и независимо от значений других символов. При передаче безызбыточных сигналов по каналу с ошибками любая принятая последовательность соответствует возможному сообщению, но полной уверенности в том, что именно это сообщение передано в действительности, у получателя нет. Признаков ошибочности принятая последовательность не может иметь.
Избыточность в передаваемом сообщении позволяет в некоторых случаях обнаруживать и исправлять ошибки. Искаженная кодовая последовательность может иметь нулевую или очень близкую к нулю вероятность, что указывает на наличие ошибки. Если определить, какая из возможных переданных последовательностей наиболее правдоподобна, можно во многих случаях ошибки исправить.
Простейшим корректирующим кодом является код с четным числом единиц. Образуется путем добавления к комбинации К-элементного кода одного избыточного элемента, чтобы количество единиц в новой N-элементной комбинации было четным. Код обнаруживает ошибку нечетной кратности. Все разрешенные комбинации имеют четное число единиц, а неразрешенные - нечетное.
Избыточность кода - относительное число избыточных элементов в кодовом слове:
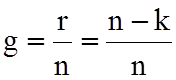r=1 k=7 n=8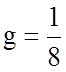 
Вероятность необнаружения ошибки равна
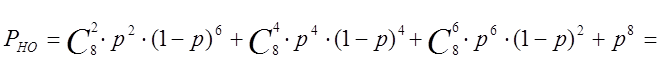
=28·0,00083082·(1-0,00083086)+70·0,00083084·(1-0,0008308)4+
+28·0,00083086·(1-0,0008308)2+0,00083088=1,923∙10-5
Количество информации
В теории информации исходят из того, что количество информации I(xi) в некотором сообщении xi зависит не от конкретного содержания, cтепени важности и т.п., а от того, каким образом выбирается это сообщение из общей совокупности возможных сообщений.
При определении количества информации исходят из следующих требований:
1. Количественная мера информации должна обладать свойство аддитивности: количество информации в нескольких независимых сообщениях должно равняться сумме количества информации в каждом сообщении.
2. Количество информации о достоверном событии (P(xi)=1) должно равняться нулю, так как такое сообщение не увеличивает наших знаний о данном объекте или явлении.
Указанным требованиям удовлетворяет
логарифмическая мера, определяемая формулой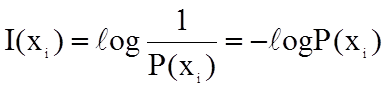 
Основание логарифма чаще всего выбирается равным 2. Полученная при этом единица информации носит название двоичная единица или бит. Количество информации в сообщении тем больше, чем оно менее вероятно.
Энтропией источника дискретных сообщений называется среднее количество информации приходящееся на одно сообщение независимого источника:
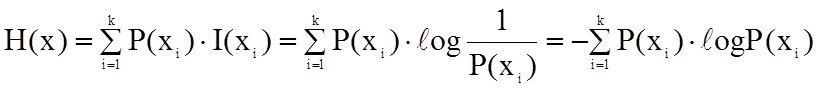
Размерность энтропии – количество единиц информации на символ. Энтропия характеризует источник сообщений с точки зрения неопределенности выбора каждого сообщения.
В соответствии с заданием Р(1)=0,9 Р(0)=0,1
бит
Избыточность источника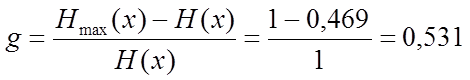 
бит
Производительность источника H'(x)=H(x)/T=0,469/4∙10-6=117250 бит/с
7.Пропускная способность канала связи
Для симметричного канала связи с основанием кода “2” пропускная способность кана -ла равна:
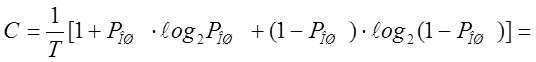
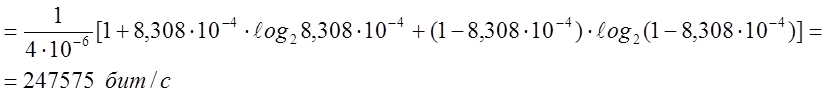
Пропускная способность канала связи достаточно велика для передачи информации по заданному каналу связи.
Заключение
Система с фазовой модуляцией позволяет получить минимальную вероятность ошибки. Помехоустойчивое кодирование позволяет повысить верность приема, статистическое кодирование обеспечивает повышение производительности источника. Применение того или иного способа кодирования определяется видом передаваемых сигналов. Так как речевые сигналы имеют высокую избыточность, при их обработке имеет смысл применить статистическое кодирование.
Список литературы
1. Зюко А.Г., Кловский Д.Д. Теория передачи сигналов.-М.: Радио и связь, 1986
2. Макаров А.А., Чиненков Л.А. Основы теории помехоустойчивости сигналов. Новосибирск 1997
3. Макаров А.А., Чиненков Л.А. Основы теории передачи информации. Новосибирск 1998.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.