Разработка структурной схемы системы связи, предназначенной для передачи данных и передачи аналоговых сигналов методом ИКМ для заданного вида модуляции и способа приема сигналов, страница 3

где Еэ - энергия разности сигналов S1(t)-S2(t), называемая "эквивалентной энергией", а Nо - спектральная плотность мощности помехи. Для конкретных видов модуляции эквивалентную энергию  определяют через энергию одного из сигналов, а в окончательные формулы вводят величину 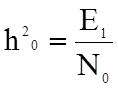 - это и значит, что в приемнике Котельникова вероятность ошибки зависит от отношения энергии сигнала к спектральной плотности помехи. Это позволяет, не меняя мощности сигнала, увеличивать его энергию за счет увеличения длительности (в неоптимальном приемнике Рош зависит от отношения мощности сигнала к мощности помехи).

Потенциальная помехоустойчивость для приемников с различными видами модуляции.

Для дискретной амплитудной модуляции S1(t)=Acosω_ot, S2(t)=0, 0<t<T

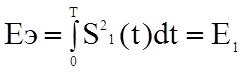 (т.е. Еэ равна энергии первого сигнала).

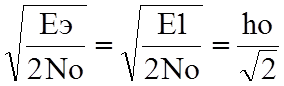
Подставив это выражение в общую формулу для вероятности ошибки, получим:

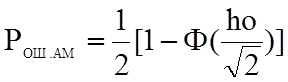
Для дискретной частотной модуляции S1(t)=Acosw1t, S2(t)=Acosw2t, 0<t<T.

Эквивалентная энергия для ДЧМ равна Еэ=2Е1,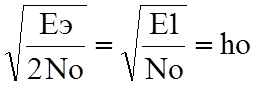

Pош чм=0.5[1-Ф(ho)]

Для дискретной фазовой модуляции:

S1(t)=AcosWot, S2(t)=-AcosWot=-S1(t), 0<t<T.

 

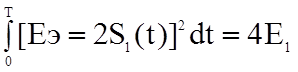
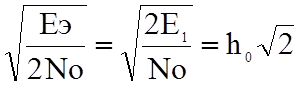
После подстановки в общую формулу получим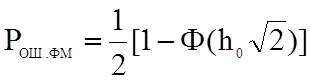

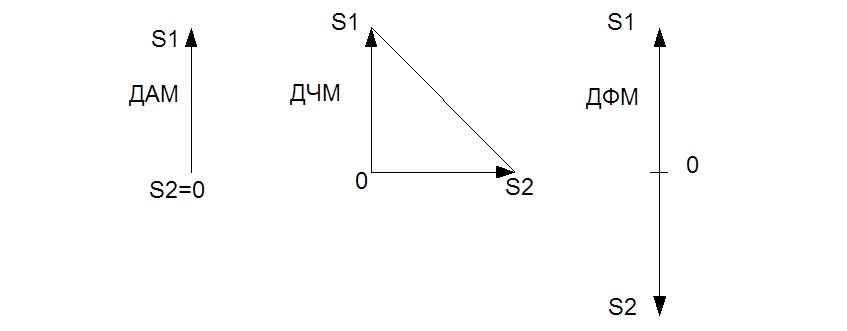Рис.6  Векторные диаграммы сигналов для различных видов модуляции

Из сравнения между собой формул для значений вероятности ошибки и векторных диаграмм для различных видов модуляции видно, что для достижения заданной вероятности ошибки требуется при ДЧМ величина ho в  раз больше, чем при ДФМ, а при ДАМ ho в 2 раза больше, чем при ДФМ, т.е. при ДЧМ получаем двукратный выигрыш по мощности по сравнению с ДАМ, а при ДФМ четырехкратный выигрыш по сравнению с ДАМ.

При одинаковой средней мощности сигналов амплитудная модуляция не имеет проигрыша по сравнению с частотной, а по сравнению с фазовой имеет проигрыш в два раза по мощности. Тем не менее при применении частотной модуляции помехоустойчивость значительно возрастает по сравнению с амплитудной модуляцией. Это объясняется тем, что оптимальная решающая схема для частотной модуляции реализуется с довольно большой точностью, а при амплитудной модуляции этому препятствует невозможность обеспечить точное оптимальное значение ненулевого порогового уровня λо. Поэтому реальная помехоустойчивость при частотной модуляции близка к оптимальной, а при амплитудной значительно ниже ее.

На рис.7 графически сравниваются различные виды модуляции: при ДАМ расстояние между векторами сигналов S1 и S2 равно длине вектора S1, при ДЧМ это расстояние равно , при ДФМ это расстояние равно 2S1. Энергия пропорциональна квадрату разности сигналов.

Для оптимального ОФМ приемника при Рс=3,2 мВт и Т=4 мкс вероятность ошибки равна

где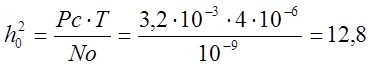

(у неоптимального ОФМ приемника Рош=8,308∙10^-4).

Оптимальная фильтрация дискретных сигналов

Возможно построение оптимального приемника с использованием в схеме когерентного приемника оптимального фильтра, в котором реализуется функция корреляции принимаемого сигнала x(t) и ожидаемого S(t).

Критерий оптимальности фильтра - максимальное отношение сигнал/шум.

Отношение сигнал-помеха для оптимального фильтра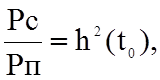

где Pс=y(to) - мощность сигнала на выходе фильтра в момент to,

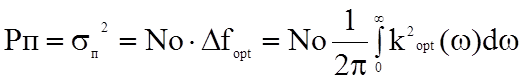 - мощность (дисперсия) помехи на выходе фильтра.

Δfopt - эффективная полоса пропускания оптимального фильтра.

,

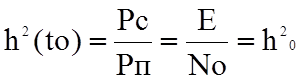где Е - энергия сигнала S(t) на входе фильтра.

Отношение ho равно отношению энергии сигнала к спектральной плотности помехи (как и в приемнике Котельникова) и не зависит от формы сигнала. Т.к. энергия сигнала равна произведению мощности сигнала на его длительность, то для повышения помехоустойчивости систем связи с использованием оптимальных фильтров можно увеличивать длительность элементарных сигналов.

Импульсная характеристика оптимального фильтра:

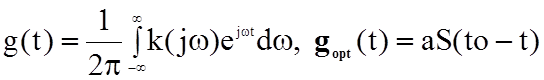
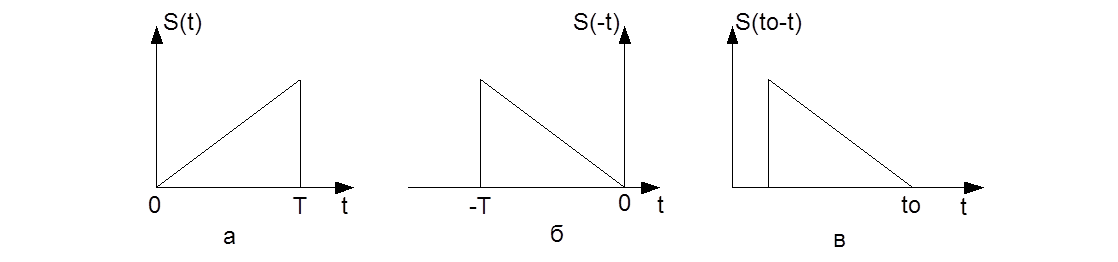
т.е. функция g(t) отличается от сигнала S(t) только постоянным множителем а, смещением на величину to (обычно to равно длительности сигнала) и знаком аргумента t - функция g(t) является зеркальным отображением сигнала S(t), сдвинутым на to: