Оптимальный приемник обеспечивает максимальную помехоустойчивость при данном способе передачи и данном виде помех.Оптимальный приемник-это приемник, наилучшим образом с точки зрения заданного критерия качества использующий известные параметры сигнала для определения (измерения) неизвестного параметра сигнала.
Оптимальный приемник в отличие от неоптимального - это когерентный приемник, в котором применяется интегратор (в приемнике Котельникова) или оптимальный фильтр.
Критерии качества помехоустойчивости приемников
S1(t), S2(t)-передаваемые сигналы.
y(t)=Si(t)+п(t)-сигналы на входе приемника; п(t)-помеха.
а) Критерий минимального среднего риска:
Оптимальной считается решающая схема, обеспечивающая наименьшее значение среднего риска Rср=П12·Р(S1)·Р(y2/S1)+П21·Р(S2)·Р(y1/S2). Приемник должен принимать решение таким образом, чтобы получить минимум Rср при заданных весовых коэффициентах П12 и П21.
б) Критерий идеального наблюдателя (критерий Котельникова)
Данный критерий минимизирует среднюю вероятность ошибки. При П12=П21
Рош=Р(S1)·Р(y2/S1)+Р(S2)·Р(y1/S2)
в) Критерий Неймана-Пирсона
Решающая схема считается оптимальной, если при заданной вероятности ложной тревоги обеспечивается минимальная вероятность пропуска сигнала
Задается вероятность пропуска сигнала S1, т.е. P(y2/S1)=a. Tогда минимизируется условная вероятность P(y1/S2) при обеспечении заданного значения а.
г) Критерий максимального правдоподобия. Этот критерий минимизирует потери информации lп=Р(y1/S2)+Р(y2/S1). Получается из критерия минимального среднего риска при условии
П12=1/P(S1), П21=1/P(S2).
Применяется, когда необходимо уменьшить вероятность искажения того сигнала, вероятность передачи которого меньше, а также при неизвестных априорных вероятностях P(S1) и P(S2).
Оптимальный приемник полностью известных сигналов
Алгоритм работы оптимального приемника
Оптимальный приемник – это такой приемник, который обеспечивает максимальную помехоустойчивость при данном способе передачи (данном виде сигнала) и данном виде помех. Оптимальный приемник полностью известных сигналов использует все параметры сигнала, не несущие информацию. Пусть S1(t)=Acos w1t, S2(t)=Acos w2t, 0<=t<=T. Оптимальный приемник (идеальный приемник Котельникова) работает следующим образом:
1. Находится ![]() и
если λ(x)>λo, то принимается решение в пользу сигнала S1, иначе S2.
Для упрощения решения полагаем, что P(S1)=P(S2)=0,5.
Тогда λо=1. В этом случае критерий максимального правдоподобия и критерий идеального
наблюдателя совпадают.
и
если λ(x)>λo, то принимается решение в пользу сигнала S1, иначе S2.
Для упрощения решения полагаем, что P(S1)=P(S2)=0,5.
Тогда λо=1. В этом случае критерий максимального правдоподобия и критерий идеального
наблюдателя совпадают.
2. Предполагаем, что на вход приемника поступает сигнал x(t)=S1(t)+п(t). Берется k отсчетов сигнала через одинаковые интервалы Δt, равные интервалу корреляции помехи τoп и рассматриваются отсчетные значения суммы сигнала S1(t) и помехи п(t) в различных сечениях ti. Получаем, что оптимальное правило решения имеет вид:
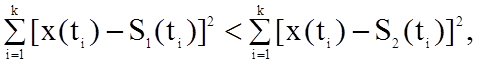 то S1.
то S1.
В интегральной форме это выражение:
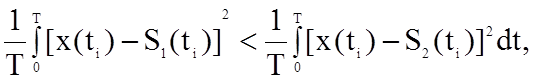 то S1.)
то S1.)
В компактной форме:
если ![]() то S1.
Если вероятности передачи сигналов S1(t) и S2(t) не одинаковы, то неравенство
принимает вид:
то S1.
Если вероятности передачи сигналов S1(t) и S2(t) не одинаковы, то неравенство
принимает вид:
![]() то S1.
то S1.
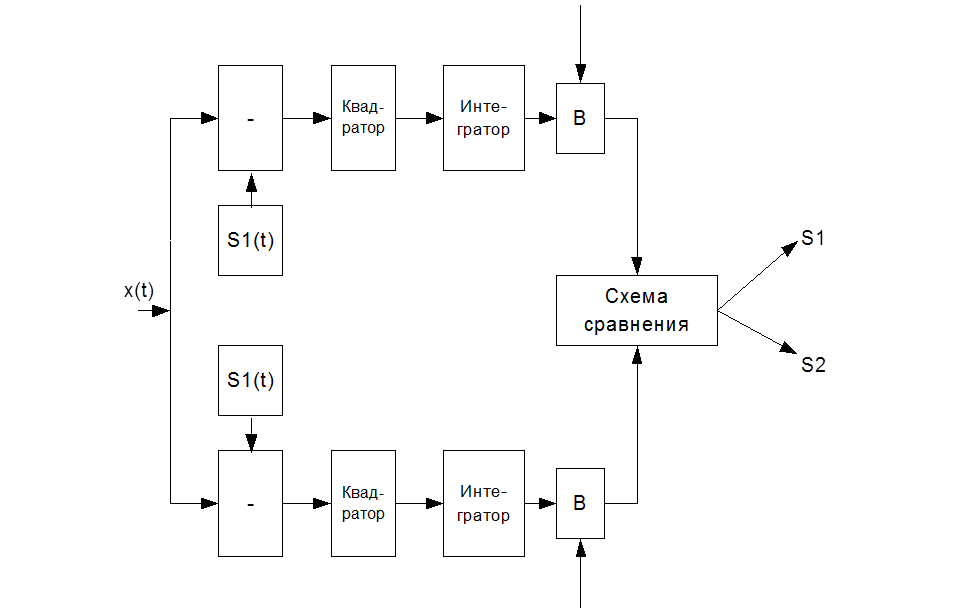
Полученному правилу соответствует структурная схема приемника:
-2σП2LnP(S1)
-2σП2LnP(S2)
Рис.5. Структурная схема оптимального приемника
Сложность реализации в том, что генераторы S1(t) и S2(t) должны выдавать сигналы, идентичные по форме сигналам, ожидаемым на входе приемника, поэтому эти генераторы должны синхронизироваться приходящими сигналами.
Оптимальный некогерентный ОФМ приемник содержит вместо ФНЧ оптимальный фильтр.
Вероятность ошибки в оптимальном приемнике
В
приемнике Котельникова вероятность ошибки зависит не от отношения мощности
сигнала к мощности помехи, а от отношения энергии сигнала к спектральной
плотности помехи. Для оптимального ОФМ приемника 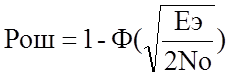
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.