Определение равенств, используя свойства операций над множествами, страница 4

г) Обозначим ребра и найдем матрицу инцидентности графа:

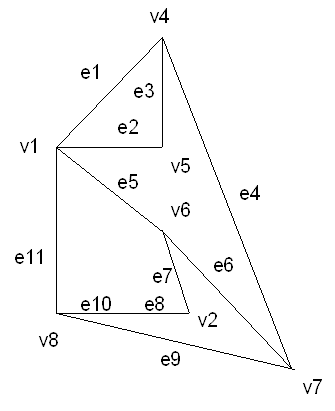
		1	2	3	4	5	6	7	8	9	10	11
	1	1	1	0	0	1	0	0	0	0	0	1
	2	0	0	0	0	0	0	-1	1	0	0	0
	3	0	0	0	0	0	0	0	-1	0	1	0
I(G)=	4	-1	0	+1	+1	0	0	0	0	0	0	0
	5	0	-1	-1	0	0	0	0	0	0	0	0
	6	0	0	0	0	-1	-1	1	0	0	0	0
	7	0	0	0	-1	0	1	0	0	-1	0	0
	8	0	0	0	0	0	0	0	0	1	-1	1

д) Определим количество компонент связности графа:

Граф называется связным, если любые две вершины U и V в нем можно соединить (u,v) маршрутом.

е) Найдем четыре простых цикла, началом и концом которого будет первая вершина:

1)  (1, 4, 5, 1)

2)  (1, 4, 7, 6, 1)

3)  (1, 6, 7, 8, 1)

4)  (1, 6, 2, 3, 8, 1)

ж) Найти минимальный остов графа и его вес.

ЗАДАЧА № 8. (151)

Найти минимальный автомат, эквивалентный данному.

	0	1
1	2,1	6,0
2	8,1	1,1
3	9,0	3,1
4	7,0	2,1
5	9,0	7,1
6	8,0	2,1
7	1,0	5,1
8	1,0	3,1
9	2,1	4,0

1)  Разбиваем множество состояний на три класса по выходным символам:

3, 4, 5, 6, 7, 8;

1, 9;

2.

2)  Рассмотрим переходы в новые состояния для класса  3, 4, 5, 6, 7, 8 при выходном символе 0:

3, 4, 5, 6, 7, 8  à⁰ 9, 7, 9, 8, 1, 1.

Состояния 7,8 принадлежат одному классу, а состояния 1,9 другому, следовательно делаем разбиение класса 3, 4, 5, 6, 7, 8  на два новых класса 3, 5, 7, 8  и  4, 6.

После этого шага имеем четыре класса:

      3, 5, 7, 8

      1, 9

      2

      4, 6

3)  Рассмотрим переходы в новые состояния для класса 3, 5, 7, 8 при выходном символе 1:

3, 4, 5, 6, 7, 8  ๠9, 7, 9, 8, 1, 1.

Так, как состояния 3, 5, 7, 9 находятся в одном классе, новых разбиений не получаем.

4)  Рассмотрим переходы в новые состояния для класса 4, 6 при входном символе 1:

            4, 6 ๠2, 2 Нового разбиения не получаем.

5)  Рассмотрим переходы в новые состояния для класса 1, 9 при входном символе 0:

1, 9  à⁰  2, 2  Нового разбиения не получаем.

6)  Рассмотрим переходы в новые состояния для класса 1, 9 при входном символе 1:

1, 9  ๠4, 6  Нового разбиения не получаем.

Окончательно разбиение на классы принимает вид:

Таблица переходов минимального автомата:

	0	1
A	C,0	A,1
B	A,0	D,1
C	D,1	B,0
D	A,1	B,1

Состоянию А минимального автомата

                  соответствует класс 3, 5, 7, 8;

Состоянию В – класс 4, 6;

Состоянию С – класс 1, 9;

Состоянию D – класс 2.

Список использованной литературы:

1. Галкина М.Ю., Дискретная математика. Программа, методические указания и задания для контрольной работы., Новосибирск, СибГУТИ, 2002.
2. Горбатов В.А, Основы дискретной математики. М.: Высшая школа, 1986 г.
3. Насыров З.Х. Дискретная математика. – Обнинск, 1999.- 125с.