Математика \ Дискретная математика

Определение равенств, используя свойства операций над множествами, страница 2

Отношения

Область определения

Множество значений

R={(4,1)};

dR = {4};

rR = {1};

P={(1,2)(2,1)(2,4)(4,2)};

dP = {1,2,4};

rP = {1,2,4};

S={(4,1)};

dS = {4};

rS = {1};

Задача № 3. (50)

Число 1123456780000

Решение: выделим все образуемые числа  по цифре, стоящей на первом месте в числе. Таких групп будет восемь, т. к. числа могут начинаться с-1,2,3,4,5,6,7,8.

1 группа: Числа из этой группы начинаются с  «1».

«1» и 000 - такое число может быть только одно.

 «1» и 00 и любые цифры из 1,2,3,3,5,6,7,8.

С23*8 = 8*(3! / (2!*1!)) = 24

 «1» и все три цифры разные из 1,2,3,4,5,6,7,8,0.

А39 = 9! / (9-3)! = 9! / 6! = 504

m1 = 1 + 24 +504 = 529.

2 группа: Числа из этой группы начинаются с  «2».

«2» и 000 - такое число может быть только одно.

«2» и 11 и любые цифры из 2,3,3,5,6,7,8,0.

 С23*8 = 8*(3! / (2!*1!)) = 24

«2» и 00 и любые цифры из 1,2,3,3,5,6,7,8.

С23*8 = 8*(3! / (2!*1!)) = 24

 «2» и все три цифры разные из 1,2,3,4,5,6,7,8,0.

А39 = 9! / (9-3)! = 9! / 6! = 504

m2 = 1 + 24+24 +504 = 553.

Числа,  начинающиеся с  3,4,5,6,7,8 находятся также, как, и числа  начинающиеся с 2.

М = m1 +  m2 * 7 = 529 + 553 * 7 = 4400

Общее количество четырехзначных чисел, образованных из цифр числа 1123456780000, равно    4400.

Задача № 4. (75)

Найти количество положительных трехзначных чисел:

а) не делящихся ни на одно из чисел; где a=3, b=8, c=20

б) делящихся ровно на одно число из чисел a,b,c.

            Обозначим:    Р3 – свойство делимости на 3;

                                    Р8 – свойство делимости на 8;

                                    Р20 – свойство делимости на 20;

            Тогда:

                                    N3 = [999/3]-[99/3]=333-33=300;

                                    N8 = [999/8]-[99/8]=124-12=112;

                                    N20 = [999/20]-[99/20]=49-4=45;

Так, как N3,8 – число чисел, делящихся одновременно на 3 и 8, а наименьшее общее кратное 8 и 3 равно 24, то :

                                    N3,8= [999/20]-[99/24]=41-4=37

            Аналогично :

                                    N3,20= [999/60]-[99/60]=16-1=15

N8,20= [999/40]-[99/40]=24-2=22

N3,8,20= [999/120]-[99/120]=8-0=8

            По формуле [1] находим искомое число чисел, делящихся ровно на одно число из чисел a,b,c:

           

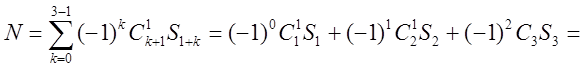
=(N3+N8+N20)-2(N3,8+N3,20)+3N3,8,20=(300+112+45)-2(37+15+22)3·8=457-148+24=333

Количество положительных 3-х-значных чисел не делящихся на a,b,c равно: 999-99-333=567.

Задача № 5. (94)

Дано: an+2 – 7an+1 + 12an = 0; a1 = -15; a2 = 15;

Составим характеристический многочлен и найдем его корни:

λ2 - 7λ +12 = 0;

D = 49 – 48 = 1

λ1 = (7 + 1)/2 = 4

λ2 = (7 - 1)/2 = 3.

Следовательно, общее решение рекуррентного соотношения имеет вид:

an = (4)n c1 + (3)n c2;

Используя начальные условия, получим систему и решим ее:

ì-15 = 4с1 +3с2;

í

î15 = 16с1 + 9с2;

ìс1 = (-15 – 3с2 )/4;

í

î15 = 16((-15 – 3с2 )/4) + 9с2;

ìс1 = 15;

í

îс2 = -25;

Таким образом:

an = 15*(4)n – 25(3)n;

Задача № 6. (113)

f(x1, x2, x3, x4) = V1(0,1,3,4,5,8,9,10,12,15)

Составим таблицу:

0

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

F

0

1

1

1

0

1

0

1

1

0

1

1

1

0

0

1

0000

0001

0010

0011

0100

0101

0110

0111

1000

1001

1010

1011

1100

1101

1110

1111

Найдем СКНФ:

СКНФ составляем по тем наборам, на которых функция принимает значение ноль.

СКНФ = (x1 ν x2 ν ¬x3 ν x4) (x1 ν ¬x2 ν ¬x3 ν x4) (x1 ν ¬x2 ν ¬x3 ν ¬x4) (¬x1 ν x2 ν ¬x3 ν x4)  (¬x1 ν¬ x2 ν x3 ν¬ x4) (¬x1 ¬ν x2 ν¬ x3 ν x4)

Найдем СДНФ:

СДНФ составляем по тем наборам, на которых функция принимает значение единица.

СДНФ = ¬x1¬x2¬x3¬ x4  ν ¬x1¬x2 ¬x3x4  ν ¬x1¬x2 x3 x4  ν ¬x1 x2¬x3¬ x4  ν ¬x1 x2 ¬x3 x4 ν  x1¬x2¬x3¬x4  ν  x1¬x2¬ x3x4   ν  x1¬x2 x3 ¬x4   ν  x1 x2¬x3¬x4  ν  x1 x2 x3 x4

Скачать файл