Примечание: ¬x – отрицание x
Найдем минимальную ДНФ с помощью карт Карно:
x1
 |
|
|
1 |
1 |
1 |
||
|
 1
|
1 |
1 |
|||
|
 1
|
1 |
||||
|
|
1 |
x2
Ответ: (x1 x2 x3 x4) ν (¬x 3¬x4 )ν (x1 ¬x2 ¬x4 )ν(¬x1¬x3 ) v (¬x2 ¬x3) ν (¬x1 ¬x2 x4 )
Найдем минимальную ДНФ методом Квайна.
Составим класс К0. В этот класс войдут все наборы, на которых функция принимает значение равное 1.
0000
0001
0011
0100
К0 = 0101
1000
1001
1010
1100
1111
Разобьем класс К0 на подклассы К0i по количеству единиц в наборе, при этом i – количество единиц в наборе.
0001* 0011*
К01 =
0100* К02 = 0101* К03 =
0000* К04 = 1111
1000* 1001*
1010*
1100*
Произведем склеивание наборов из соседних подклассов, наборы, участвующие в склеивании пометим звездочкой. Наборы, полученные при склеивании разобьем по месту расположения ‘х’ .
х000* 0х00* 00х1
000x*
К11 =
х001* К12 = 0х01* К13 =
10х0 К14 = 010х*
х100* 1х00* 100х*
Произведем склеивание наборов в каждом подклассе. В полученных наборах вычеркнем повторяющиеся наборы и окончательно получаем:
1111, xx00, x00x, 0x0x, 00x1,10x0.
Построим таблицу:
|
|
0000 |
0001 |
0011 |
0100 |
0101 |
1000 |
1001 |
1010 |
1100 |
1111 |
|
|
V |
|||||||||
|
|
V |
V |
V |
v |
||||||
|
|
V |
V |
V |
V |
||||||
|
|
V |
V |
V |
V |
||||||
|
|
V |
V |
||||||||
|
|
V |
V |
Ответ: (x1 x2 x3 x4) ν (¬x 3¬x4 )ν (x1 ¬x2 ¬x4 )ν(¬x1¬x3 ) v (¬x2 ¬x3) ν (¬x1 ¬x2 x4 ).
Граф G задан списком ребер (каждый элемент списка – это тройка чисел: номера двух смежных вершин и вес ребра, их соединяющего).
|
(1,4,8), (1,5,4), (1,6,6), (1,8,3), (2,3,1), (2,6,5), (3,8,7), (4,5,9), (4,7,2), (6,7,5), (7,8,1) |
Требуется:
а) Нарисовать граф G.
б) Найти степенную последовательность графа G.
в) Найти матрицу смежности графа G.
г) Обозначить ребра и найти матрицу инцидентности графа.
д) Определить количество компонент связности графа.
е) Найти четыре простых цикла.
ж) Найти минимальный остов графа и его вес.
Решение: а) нарисуем граф G:
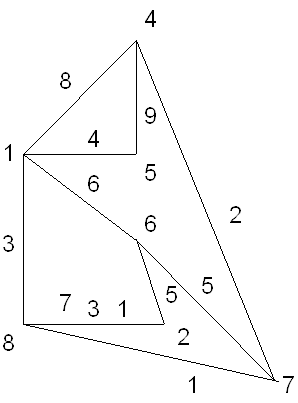
б) находим степенную последовательность графа, для этого выпишем степени вершин в соответствии с их номерами: (4, 2, 2, 3, 2, 3, 3, 3);
в) находим матрицу смежности графа G:
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
||
|
1 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
|
|
2 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
|
|
3 |
0 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
|
|
А(G)= |
4 |
1 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
|
5 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
6 |
1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
|
|
7 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
8 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
0 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
1
1111
Xx00
X00x
0x0x
00x1
10х0