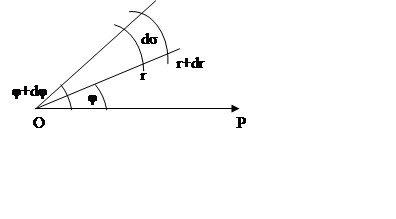
![]() , где S1 и S2 –
площади 2-х секторов.
, где S1 и S2 –
площади 2-х секторов.
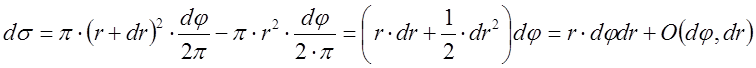 , где
, где 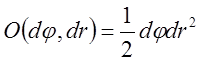 – бесконечно малая величина третьего
порядка и
– бесконечно малая величина третьего
порядка и ![]() .
.
В результате двойной интеграл в полярной системе координат имеет вид
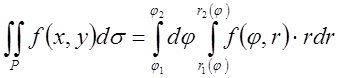 , где
Р:
, где
Р: 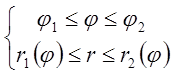 .
.
Тройной интеграл. Задача о заряде тела.
Пусть дано тело, объём которого равен V, состоящее из заряженного вещества, с плотностью заряда q(x, y, z), изменяющийся от точки к точке в пределах этого тела. Требуется найти заряд Q этих точек.
Разложим тело на ряд ΔV1, ΔV2,…, ΔVi частичных объёмов и в каждой части выберем произвольную точку M(εi,ξi,ζi).
Плотность заряда в этой точке q(εi,ξi,ζi). Пологая, что плотность заряда в пределах объёма ΔVi постоянна, найдём заряд ΔQi этого объёма
![]() .
.
Тогда приближенно заряд тела Q равен
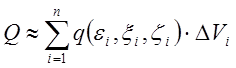 .
Устремив
.
Устремив ![]() , получим точно значение
, получим точно значение 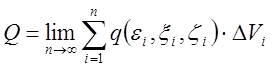 .
.
Как обычно, если этот предел существует и не зависит от способа разбиения и выбора точки (εi,ξi,ζi), то он называется тройным интегралом функции q(x, y, z) по объёму V.
Эту же задачу решим при ином способе разбиения объёма интегрирования V.
С этой целью конкретизируем
объём интегрирования. Пусть тело является цилиндрическим, ограниченным снизу и
сверху, соответственно, поверхностями (![]() ,
, ![]() ) (точки входа и выхода), проектирующимся на плоскость xOy,
в некоторую область Р. С боков это тело ограничено цилиндрической поверхностью
с образующими, параллельными оси Oz.
) (точки входа и выхода), проектирующимся на плоскость xOy,
в некоторую область Р. С боков это тело ограничено цилиндрической поверхностью
с образующими, параллельными оси Oz.
Проведём плоскости ![]() ,
, ![]() ,
аппликаты которых удовлетворяют неравенству
,
аппликаты которых удовлетворяют неравенству ![]() . При этом получаем цилиндрическое тело с высотой Δz. Рассечём
на плоскости xOy область Р на области Р1, Р2,…,
Рn, которых Δσ1, Δσ2,…, Δσn,
соответственно, и через стороны этих областей проведём плоскости, параллельно
оси Oz до пересечения с основаниями цилиндрического тела
высотой Δz. Получим n тел, объёмы которых равны
. При этом получаем цилиндрическое тело с высотой Δz. Рассечём
на плоскости xOy область Р на области Р1, Р2,…,
Рn, которых Δσ1, Δσ2,…, Δσn,
соответственно, и через стороны этих областей проведём плоскости, параллельно
оси Oz до пересечения с основаниями цилиндрического тела
высотой Δz. Получим n тел, объёмы которых равны ![]() . В
каждом из этих объёмов возьмём точку (εi,ξi,ζi)
и определим в ней плотность заряда q(εi,ξi,ζi).
Тогда заряд i-ого тела равен
. В
каждом из этих объёмов возьмём точку (εi,ξi,ζi)
и определим в ней плотность заряда q(εi,ξi,ζi).
Тогда заряд i-ого тела равен ![]() , заряд
Q всего тела приближённо равен
, заряд
Q всего тела приближённо равен 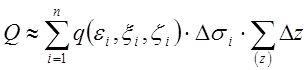 .
.
Устремив Δσi
и Δzi к нулю, получим точную величину заряда тела 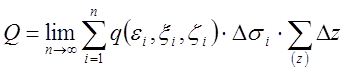 или по привычным ранее использовавшимся
определениям
или по привычным ранее использовавшимся
определениям
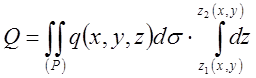 , где
первый интеграл двойной, второй – определённый. Так как Δσ в декартовой
прямоугольной системе координат имеет вид
, где
первый интеграл двойной, второй – определённый. Так как Δσ в декартовой
прямоугольной системе координат имеет вид ![]() ,
получим повторный интеграл
,
получим повторный интеграл 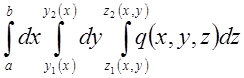 , равный тройному интегралу.
Здесь объём V (предел интегрирования) заданы в виде элементарных
неравенств
, равный тройному интегралу.
Здесь объём V (предел интегрирования) заданы в виде элементарных
неравенств
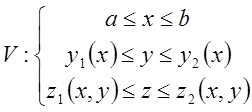 .
.
В результате получено правило вычисления тройного интеграла (сведение его к повторному). Сначала задаётся в виде простейших неравенств объём тела интегрирования (определяются пределы интегрирования), затем повторно (справа на лево) вычисляются 3 определённых интеграла:
1) 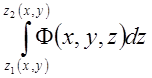 –
при постоянных x и y;
–
при постоянных x и y;
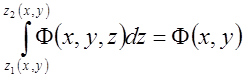 и
далее.
и
далее.
2) 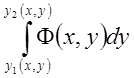 –
при
–
при ![]()
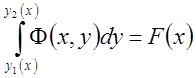 и
далее.
и
далее.
3) 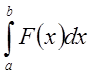 .
.
Цилиндрическая система координат.
Цилиндрическая система координат представляет собой полярную систему координат на плоскости Р и ось Oz, перпендикулярную к плоскости Рn, проходящую через начало координат. О(0,0,0) – полюс полярной системы координат. Любая точка в этой системе координат определяется тройкой действительных чисел (φ, r, z). В результате имеют место формулы перехода из цилиндрический системы координат в декартову прямоугольную систему координат:
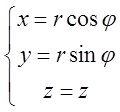 .
.
Определим координатные поверхности этой системы координат:
а) ![]() (φ0
– постоянная) при произвольном z или
(φ0
– постоянная) при произвольном z или 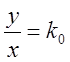 (
(![]() ) – полуплоскость, содержащая ось Oz и проходящая через луч
) – полуплоскость, содержащая ось Oz и проходящая через луч ![]() на плоскости Р;
на плоскости Р;
б) ![]() (R –
постоянная) при
(R –
постоянная) при ![]() или
или ![]() –
кривая цилиндрическая поверхность с образующей параллельной оси Oz;
–
кривая цилиндрическая поверхность с образующей параллельной оси Oz;
в) ![]() (z0 – постоянная) – плоскость, параллельная плоскость Р.
(z0 – постоянная) – плоскость, параллельная плоскость Р.
Тогда единственная точка (φ0,
R, z0) определяется как пересечение трёх
координатных поверхностей. Действительно, при ![]() и
и ![]() соответствующие полуплоскость и цилиндр
пересекаются по прямой, параллельной оси Oz. Пересекая
эту прямую координатной плоскостью
соответствующие полуплоскость и цилиндр
пересекаются по прямой, параллельной оси Oz. Пересекая
эту прямую координатной плоскостью ![]() , получаем единственную
точку с этой координатами. При этом имеют место формулы перехода из декартовой
системы координат в цилиндрическую систему координат
, получаем единственную
точку с этой координатами. При этом имеют место формулы перехода из декартовой
системы координат в цилиндрическую систему координат
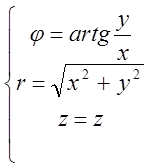 .
.
Как мы уже видели ранее,
элемент площади в полярной системе координат равен ![]() .
.
Тогда элемент объёма dV
имеет вид ![]() .
.
В результате тройной интеграл
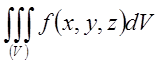 в цилиндрической системе координат
принимает вид:
в цилиндрической системе координат
принимает вид:
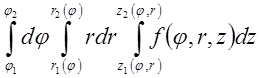 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.