Неопределенный интеграл. Основные методы интегрирования. Интегрирование рациональной дроби, страница 2

Интегрирование рациональной дроби.

Многочленом  –ой степени относительно  называется сумма

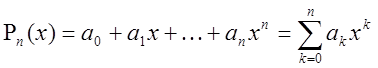,где   действительные числа-коэффициенты многочлена. Многочлен задан, если заданы его коэффициенты. Два многочлена  и  равны, если равны коэффициенты при одинаковых степенных неизвестных. При этом очевидно, что .

Рациональной дробью называется отношение двух многочленов . При этом, если    , то дробь неправильная, в противном случае

- дробь правильная. Если дробь неправильная, то делением можно выделить ее целую и дробную части.

Например : 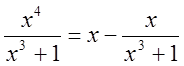 , где уменьшаемое - целая часть, вычитаемое – правильная дробь – дробная часть.

Ввиду многообразия дробей, введем простейшие дроби

.

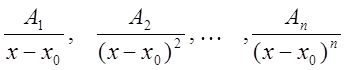Интегрирование введенных дробей не представляет трудности.

Более сложной является дробь вида 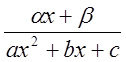. Покажем, что если дискриминант уравнения   неотрицательный  , то эта дробь сводится к уже приведенным дробям.

Поделим числитель и знаменатель на  и обозначим  .

Тогда имеем

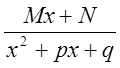
Если дискриминант , то существуют корни       квадратного уравнения . И знаменатель можно представить в виде .

Тогда

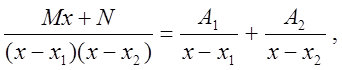
причем это равенство имеет место, если существуют постоянные

.

Приводя правую часть к общему знаменателю, получим

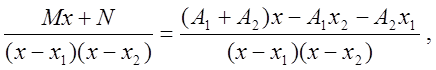
Откуда

 имеем

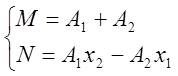
систему двух уравнений первой степени относительно . Определим коэффициенты системы

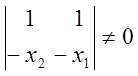, так как   и поэтому существует единственное решение   этой системы, что и требовалось доказать.

И, далее, рассмотрим     

Тогда 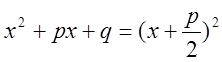  и

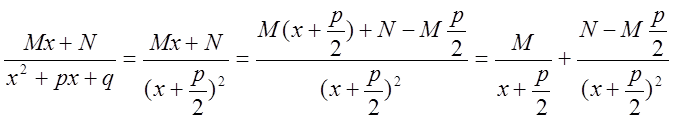
, то есть, и в этом случае дробь 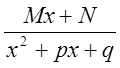 сводится к простейшим дробям. Заметим, что метод

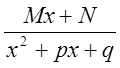
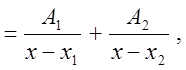
сведение сложной дроби к простейшим называется методом неопределенных коэффициентов ().

Пусть, наконец,  . Тогда имеем

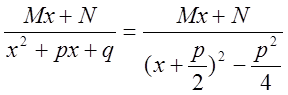
Рассмотрим интеграл от такой дроби: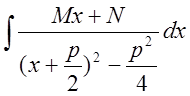

  Проведем замену переменной 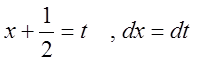  . Тогда получим

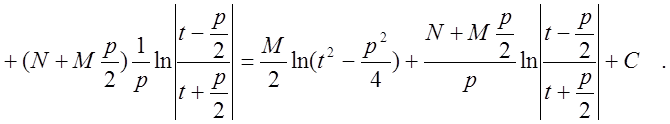
Приведем без доказательства основную теорему алгебры: всякую правильную дробь можно представить в виде суммы простейших дробей, то есть

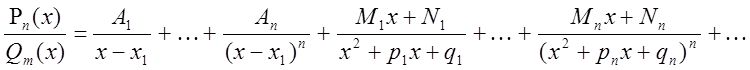
И, наконец, вычислим интеграл

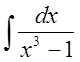. С этой целью  представим в виде . Тогда по методу неопределенных коэффициентов имеем

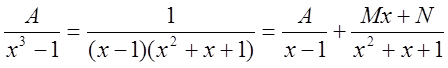
приводя к общему знаменателю и приравнивая числители, получим

отсюда

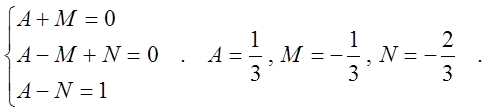
тогда

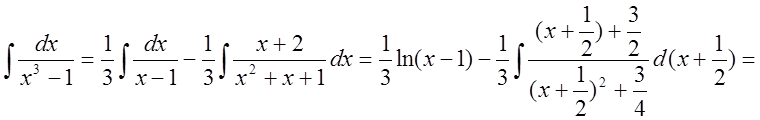
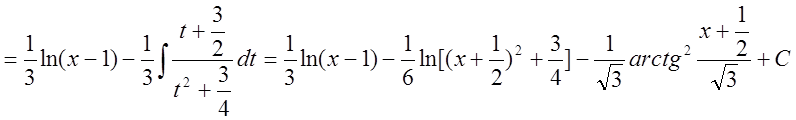
Определенный интеграл.

Ниже рассматриваются только неправильные и кусочно-непрерывные функции на некотором конечном интервале .

Функция , заданная на интервале , называется кусочно-непрерывной на этом интервале, если точками

Интервал делится на конечное число частей  , внутри которых функция непрерывна, а на концах имеет предельные значения:

Для таких функций (непрерывных и кусочно-непрерывных) существует определенный интеграл. Доказательство этого утверждения выходит за пределы курса, изучаемого в университете.

Пусть функция  непрерывна или кусочно-непрерывна  на интервале . Разобьем этот интервал на  частичных интервалов      различной длины . Внутри каждого интервала зададим значение функции

Рассмотрим число

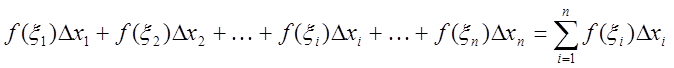
, называемое интегральной суммой функции , соответствующей данному способу разбиения интервала  и данному выбору промежуточных точек  на  частичных интервалах .

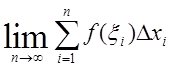Рассмотрим предел интегральной суммы когда длина наибольшего отрезка   : стремится к нулю (или ) . Если этот предел существует (равен числу) и не зависит от способа разбиения интервала  на части и выбора значения функции на этих частичных интервалах, то он называется определенным интегралом:

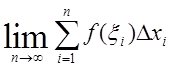
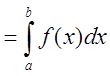
,где а и   - нижний и верхний пределы интегрирования.

Свойства определенного интеграла.

1. 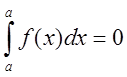 . Эта формула должна рассматриваться как соглашение.

2.     при  . Интегральная сумма левой части равенства имеет вид:

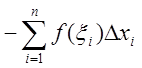   , где знак минус принадлежит всем разностям   , При этом справа имеем 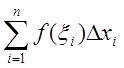 . Переходя к пределу при   , убеждаемся в справедливости этой формулы.

3.    

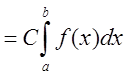
Интегральная сумма левой части равна 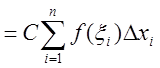, откуда следует справедливость рассматриваемой формулы.

4. Пусть для функции  и  существуют интегралы 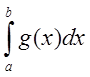. Тогда .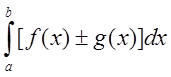

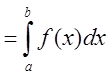
Очевидно, что

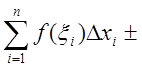
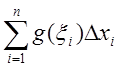
и в этом равенстве при определенном способе разбиения и   существует предел правой части. Следовательно, существует предел левой части и имеет место рассматриваемое свойство.

5.    .

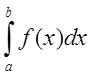
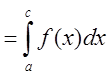
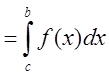Интегральная сумма левой части может быть представлена в виде