Таким образом, вычисление
этого интеграла состоит из двух этапов: на первом этапе вычисляется
определённый интеграл 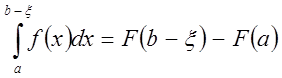 ; на втором вычисляется
предел
; на втором вычисляется
предел ![]() .
.
Очевидно, что рассмотренные два вида несобственных интегралов полностью аналогичны. Поэтому и для интегралов от неограниченных функций имеют место аналогичные теоремы: необходимый и достаточный признак сходимости, теорема сравнения и иные теоремы, не входящие в наш курс.
Кратные интегралы.
Двойной интеграл. Задача об объёме цилиндрического тела.
Рассмотрим тело, которое
сверху ограничено поверхностью ![]() , с боков –
цилиндрической поверхностью с образующими, параллельными оси Oz,
снизу – плоской фигурой Р на плоскости xOy.
, с боков –
цилиндрической поверхностью с образующими, параллельными оси Oz,
снизу – плоской фигурой Р на плоскости xOy.
Разложим плоскую область Р
сетью кривых на части Р1, Р2,…,Рn
и рассмотрим ряд цилиндрических столбиков, которые имеют своими нижними
основаниями эти частичные области, а их верхние основания вырезаются этими
столбиками на поверхности ![]() .
.
Для подсчёта объёма отдельных
столбиков возьмём произвольно в каждой фигуре Pi
точку ![]() . Если принять каждый столбик за цилиндр с
высотой, равной аппликате
. Если принять каждый столбик за цилиндр с
высотой, равной аппликате ![]() и основанием Pi с площадью σi, то приближенно объём каждого столбика равен
и основанием Pi с площадью σi, то приближенно объём каждого столбика равен ![]() .
.
Тогда приближенно объём тела V равен
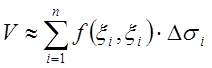
Для повышения точности
уменьшаем ![]() размеры площадки Pi,
увеличивая их число
размеры площадки Pi,
увеличивая их число ![]() , и при этом получим
, и при этом получим
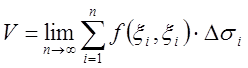 .
Задача решена.
.
Задача решена.
Предел этого вида и есть
двойной интеграл от функции ![]() по области Р:
по области Р: 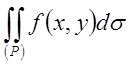 .
.
Если такой предел существует
и не зависит от способа разбиения области Р на части Pi,
от выбора на этих частях точек ![]() , то он называется
двойным интегралом от функции
, то он называется
двойным интегралом от функции ![]() по области Р.
по области Р.
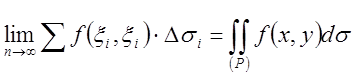 .
.
Также, как и в определённом интеграле такой предел (и двойной интеграл) существует для непрерывных и кусочно-непрерывных функций.
Установим правило вычисления двойного интеграла.
Рассмотрим тело, ограниченное
поверхностью ![]() , по плоскостям x=a, x=b, y=α, y=β ??? координатной плоскости – прямоугольником Р:
, по плоскостям x=a, x=b, y=α, y=β ??? координатной плоскости – прямоугольником Р: 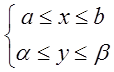 . Для произвольного значения
. Для произвольного значения ![]() тело имеет поперечное сечение, площадь
которого Q(x). Тогда
тело имеет поперечное сечение, площадь
которого Q(x). Тогда 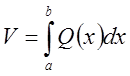 ,
, 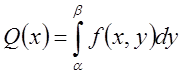 и
и 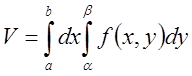 .
.
Изменим конфигурацию области
Р: 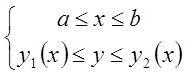 и возьмём криволинейный четырёхугольник, у
которого линии y1(x), y2(x) называются точками входа и выхода соответственно. В
более общем случае получим:
и возьмём криволинейный четырёхугольник, у
которого линии y1(x), y2(x) называются точками входа и выхода соответственно. В
более общем случае получим:
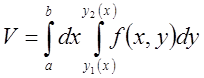 .
Интеграл такого вида называются повторными. С другой стороны, используем ранее
полученный результат
.
Интеграл такого вида называются повторными. С другой стороны, используем ранее
полученный результат 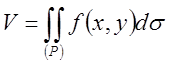 . Тогда соотношение
. Тогда соотношение 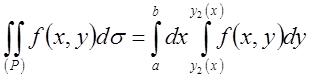 является правилом вычисления двойного
интеграла: сначала вычисляется при
является правилом вычисления двойного
интеграла: сначала вычисляется при ![]() определённый интеграл
определённый интеграл 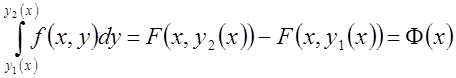 , затем
, затем 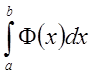 – ещё
один определённый интеграл. Отметим, что
– ещё
один определённый интеграл. Отметим, что ![]() .
.
Двойной интеграл обладает всеми свойствами определённого интеграла, поскольку он также, как и определённый интеграл определён как предел интегральных сумм:
- постоянный множитель выносится за знак интеграла;
- интеграл от суммы функций равен сумме интегралов слагаемых функций;
- двойным интегралом можно интегрировать неравенства и т. д.
Для двойного интеграла имеет
место аналогичная теорема о среднем значение, если для определённого интеграла
это значение 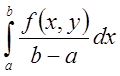 , то для двойного –
, то для двойного – 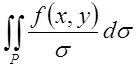 .
.
Полярная система координат.
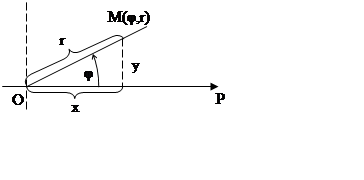 Полярная система координат имеет вид:
(см. рисунок), где точка О – начало координат, полярная
ось (О – полюс). Произвольные полупрямые (???)
наклонены под углом φ. Точка М в полярной системе имеет координаты φ и r, где r
– её расстояние от начала координат.
Полярная система координат имеет вид:
(см. рисунок), где точка О – начало координат, полярная
ось (О – полюс). Произвольные полупрямые (???)
наклонены под углом φ. Точка М в полярной системе имеет координаты φ и r, где r
– её расстояние от начала координат.
Совмещая декартову
прямоугольную систему координат с полярной системой, получим формулы перехода 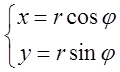 из полярной системы в декартову. Определим
координатные линии полярной системы координат. Пусть
из полярной системы в декартову. Определим
координатные линии полярной системы координат. Пусть ![]() ,
тогда
,
тогда 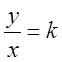
![]() и полупрямая
и полупрямая ![]() является одной из координатных линий.
Пологая постоянным r,
является одной из координатных линий.
Пологая постоянным r, ![]() , получим
, получим ![]() другую координатную линию – окружность. Их
пересечение определяет единственную точку (
другую координатную линию – окружность. Их
пересечение определяет единственную точку (![]() ;
; ![]() ) или (φ0; r0).
) или (φ0; r0).
Приведём формулу перехода из декартовой системы в полярную систему координатной
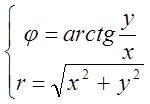 .
.
Как уже отмечалось, в
декартовой системе координат элемент площади dσ – бесконечно
малая величина второго порядка ![]() . Определим вид
элемента dσ в полярной системе координат. С этой целью, также как
и в системе xOy, построим координатные линии, отличающиеся на
величины dφ и dr. Их пересечение является элементом dσ.
. Определим вид
элемента dσ в полярной системе координат. С этой целью, также как
и в системе xOy, построим координатные линии, отличающиеся на
величины dφ и dr. Их пересечение является элементом dσ.
Рассмотрим секторы с углом dφ и радиусом r и r+dr.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.