Темы лабораторных работ по курсу «Математические методы моделирования» («Вычислительная математика»)

Темы лабораторных работ по курсу

«Математические методы моделирования»

(«Вычислительная математика»)

I семестр

Вычислительные методы линейной алгебры

1. Решение систем линейных алгебраических уравнений с квадратными матрицами общего вида.
2. Решение систем линейных алгебраических уравнений с квадратными симметричными матрицами.
3. Решение систем линейных алгебраических уравнений с квадратными симметричными положительно-определёнными матрицами.
4. Решение систем линейных алгебраических уравнений с квадратными ленточными матрицами общего вида.
5. Решение систем линейных алгебраических уравнений с квадратными симметричными ленточными положительно-определёнными матрицами.
6. Решение систем линейных алгебраических уравнений с квадратными разреженными матрицами общего вида.
7. Решение систем линейных алгебраических уравнений с квадратными симметричными разреженными положительно-определёнными матрицами.

Задание к работам 1-7

      Напишите программу для решения с обычной (а затеми с двойной) точностью системы линейных алгебраических уравнений , в которой квадратная матрица и правая часть зависят от параметра р. Параметр выбран так, что при всех его значениях  существует один и тот же вектор х.

Матрица, вектор правой части и дополнительная информация о системе уравнений содержатся в файлах, выдаваемых преподавателем.

Для решения систем использовать программы из библиотеки IMSL, входящей в состав Compaq Visual Fortran.

Применить программы из библиотеки IMSL дающие оценку числа обусловленности матрицы или его обратной величины.

Написанная программа должна выводить в файл следующие данные:

фамилию, имя и номер группы автора программы

значение параметра р,

матрицу и правую часть системы уравнений,

оценку числа обусловленности матрицы и оценку обратной величины числа обусловленности ,

найденное приближённое решение ,

вектор невязки ,

оценку погрешности решения 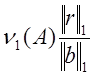 из неравенства 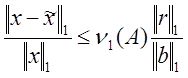, где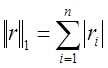

Дайте письменные ответы на следующие вопросы:

1.  Как изменяется число обусловленности матрицы с уменьшением значения параметра р?

2.  Что происходит с системой при  ?

3.  Сравните при одних и тех же значениях р решения, найденные с обычной и двойной точностью. Почему при решения отличаются больше, чем при других значениях р? Если решения при получить не удаётся, то в чём причина?

Отправьте файл преподавателю для проверки.

II семестр

1.  Вычисление всех собственных чисел и собственных векторов симметричной матрицы.

2.  Вычисление всех собственных чисел и собственных векторов несимметричной матрицы.

Аппроксимация функций, численное дифференцирование и интегрирование с использованием библиотеки IMSL

3.  Аппроксимация функций интерполяционным кубическим сплайном с помощью программы CSIEZ

4.  Аппроксимация функций и их производных интерполяционным кубическим сплайном с помощью CSINT и CSDER

5.  Аппроксимация функций интерполяционными В- сплайнами программой DBSINT

6.  Аппроксимация функции от двух переменных интерполяционными двумерными сплайнами В- сплайнами программой DBS2IN

Задание к работе 1

Напишите программу для решения с обычной (а затеми с двойной) точностью задачи на собственные значения , в которой квадратная матрица зависит от параметра р.

Информация о матрице содержится в файлах, выдаваемых преподавателем.

Для решения задачи использовать программы из библиотеки IMSL, входящей в состав Compaq Visual Fortran.

Дополнительно вычислить индекс выполнения (performance index), используя программу из библиотеки IMSL.

Написанная программа должна выводить в файл следующие данные:

фамилию, имя и номер группы автора программы

значение параметра р,

матрицу,

найденные собственные числа матрицы ,

найденные собственные векторы ,

индекс выполнения (performance index)

векторы невязок ,

проверку ортогональности собственных векторов

Дайте письменные ответы на следующие вопросы:

1. Как изменяется наименьшее по модулю собственное число матрицы с уменьшением значения параметра р?

2. Что происходит с матрицей при  ?

3. Сравните при одних и тех же значениях р решения, найденные с обычной и двойной точностью.?

4.  Что такое индекс выполнения (performance index) в библиотеке IMSL и каков его смысл ?

Задание к работе 2

Напишите программу для решения с обычной (а затеми с двойной) точностью задачи на собственные значения , в которой квадратная матрица зависит от параметра р.

Информация о матрице содержится в файлах, выдаваемых преподавателем.

Для решения задачи использовать программы из библиотеки IMSL, входящей в состав Compaq Visual Fortran.