Дополнительно вычислить индекс выполнения (performance index), используя программу из библиотеки IMSL.
Написанная программа должна выводить в файл следующие данные:
фамилию, имя и номер группы автора программы
значение параметра р,
матрицу,
найденные собственные числа матрицы ![]() ,
,
найденные собственные векторы ![]() ,
,
индекс выполнения (performance index)
векторы невязок ![]() ,
,
Дайте письменные ответы на следующие вопросы:
1. Как изменяется наименьшее по модулю собственное число матрицы с уменьшением значения параметра р?
2. Что происходит с матрицей при ![]() ?
?
3. Сравните при одних и тех же значениях р решения, найденные с обычной и двойной точностью.?
Что такое индекс выполнения (performance index) в библиотеке IMSL и каков его смысл ?
Задание к работе 3
Напишите программу с одинарной
точностью для аппроксимации заданной функции ![]()
![]() интерполяционным кубическим сплайном
интерполяционным кубическим сплайном ![]() , используя программу CSIEZ из библиотеки IMSL.
, используя программу CSIEZ из библиотеки IMSL.
Оцените погрешность аппроксимации
функции сплайном для числа разбиений интервала N=10,
20, 40, 80, 160. Погрешность аппроксимации оцените по формуле ![]() , где
, где 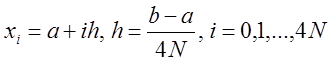 .
.
Написанная программа должна выводить в файл следующие данные:
фамилию, имя и номер группы автора программы, ![]() ,
a, b, N, и
,
a, b, N, и ![]() .
.
Для каждого N
постройте графики ![]() и
и ![]() .
.
Дайте письменные ответы на следующие вопросы:
Как изменятся погрешность ![]() с увеличением числа разбиений? Найдите
отношения погрешностей ε для двух соседних разбиений.
с увеличением числа разбиений? Найдите
отношения погрешностей ε для двух соседних разбиений.
Сравните, полученные результаты с
теоретической оценкой ![]() .
.
Задание к работе 4
Напишите
программу с одинарной точностью для аппроксимации заданной функции ![]() ,
, ![]() и её
первых трёх производных интерполяционным кубическим сплайном
и её
первых трёх производных интерполяционным кубическим сплайном ![]() , используя программы CSINT
и CSDER из библиотеки IMSL.
Вычислите
, используя программы CSINT
и CSDER из библиотеки IMSL.
Вычислите 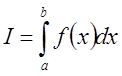 , используя CSITG.
, используя CSITG.
Оцените
погрешность аппроксимации функции, производных и интеграла сплайном для числа
разбиений интервала N=10, 20, 40, 80, 160. Погрешность
аппроксимации функции и её производных оцените по формуле ![]() , где
, где 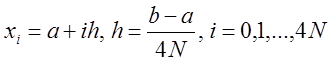 .
Погрешность вычисления интеграла
.
Погрешность вычисления интеграла 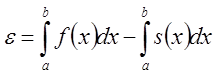
Написанная программа должна выводить в файл следующие данные:
фамилию, имя и номер группы автора программы
![]() , a, b, N,
, a, b, N,
![]() и отношения погрешностей для двух соседних
разбиений для функции, производных и интеграла.
и отношения погрешностей для двух соседних
разбиений для функции, производных и интеграла.
Для каждого N постройте графики ![]() и
и ![]() .
.
Дайте письменные ответы на следующие вопросы:
Как изменятся погрешность аппроксимации функции, производных и интеграла с увеличением числа разбиений? Сравните, полученные результаты с теоретической оценкой.
Как будет вести себя погрешность аппроксимации функции при дальнейшем увеличении N ?
Задание к работе 5
Напишите
программу с двойной точностью для аппроксимации заданной функции ![]() ,
, ![]() интерполяционными
В- сплайнами
интерполяционными
В- сплайнами 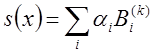 , где k-степень
сплайна, используя программы DBSINT из библиотеки IMSL.
, где k-степень
сплайна, используя программы DBSINT из библиотеки IMSL.
Оцените
погрешность аппроксимации функции сплайном для числа разбиений интервала N=10, 20, 40, 80 при k=1, 2,
3, 4, 5. Погрешность аппроксимации функции оцените по формуле ![]() , где
, где 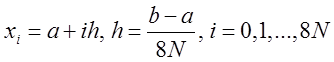 .
Написанная программа должна выводить в файл следующие данные:
.
Написанная программа должна выводить в файл следующие данные:
фамилию, имя и номер группы автора программы
![]() , a, b, N,
, a, b, N,
![]() и отношения погрешностей для двух соседних
разбиений для функции
и отношения погрешностей для двух соседних
разбиений для функции
Для
фиксированного к постройте графики ![]() и
и ![]() при различных N.
при различных N.
Дайте письменные ответы на следующие вопросы:
Как изменятся погрешность аппроксимации функции с увеличением числа разбиений для различных к?
Задание к работе 6
Напишите
программу с двойной точностью для аппроксимации заданной функции ![]() ,
, ![]() ,
, ![]() интерполяционными двумерными сплайнами В-
сплайнами, представленными тензорным произведением
интерполяционными двумерными сплайнами В-
сплайнами, представленными тензорным произведением 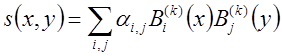 , где k-степень сплайна, используя программы DBS2IN из библиотеки IMSL.
, где k-степень сплайна, используя программы DBS2IN из библиотеки IMSL.
Оцените
погрешность аппроксимации функции и первых производных по x,
y сплайном для числа разбиений интервала N=10, 20, 40, 80 при k= 3
(кубический сплайн). Используйте функцию DBS2DR. Погрешность
аппроксимации функции оцените по формуле ![]() , где
, где 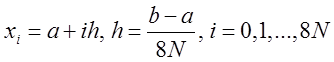 ;
; 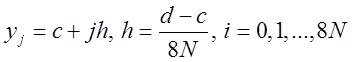 .
Написанная программа должна выводить в файл следующие данные:
.
Написанная программа должна выводить в файл следующие данные:
фамилию, имя и номер группы автора программы
![]() , a, b, c,
d, N,
, a, b, c,
d, N, ![]() и отношения погрешностей для двух соседних
разбиений для функции и первых производных.
и отношения погрешностей для двух соседних
разбиений для функции и первых производных.
Постройте
графики ![]() и
и ![]() при
различных N.
при
различных N.
Дайте письменные ответы на следующие вопросы:
Как изменятся погрешность аппроксимации функции и первых производных с увеличением числа разбиений?
Вид функций для двумерной интерполяции
1. ![]() ,
, ![]()
2. ![]() ,
, ![]()
3. ![]() ,
, ![]()
4. ![]() ,
, ![]()
5. ![]() ,
, ![]()
6. ![]() ,
, ![]()
7. ![]() ,
, ![]()
8. ![]() ,
, ![]()
9. ![]() ,
, ![]()
10. ![]() ,
, ![]()
11. ![]() ,
, ![]()
12. ![]() ,
, ![]()
13. ![]() ,
, ![]()
Таблица 1. Вид функций для одномерной интерполяции
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.