Процесс перегонки жидкостей. Ректификация, страница 3

Для идеальных растворов справедливы уравнения Рауля и Генри. Графическое изображение закона Рауля дает рис. 3. Согласно уравнению Рауля:

p_i = P_i·x'_i,                                    (2)

где р_i — парциальное давление компонента;

х¢_i — его молярная доля в жидкой фазе;

P_i — упругость пара чистого компонента при заданной температуре.

По закону Генри растворимость газов и паров в жидкости при постоянной температуре прямо пропорциональна давлению газа (пара) над раствором. Математически этот закон может быть записан так:

x'_i = K¢_i·p_i,                                  (3)

где х¢_i — концентрация компонента в молярных долях в жидкости;

К¢_i — константа;

p_i — парциальное давление паров рассматриваемого компонента.

Это уравнение может быть записано и так:

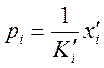  или                            (4)

Из сопоставления уравнений (2) и (4) видно, что для идеального раствора K_i = P_i т. е. константа Генри K_i совпадает с давлением пара чистого компонента при данной температуре.

Уравнения Рауля и Генри применимы ко многим реальным системам и могут быть использованы в расчетах с достаточной точностью. В частности, они применяются для расчетов ректификации смеси углеводородов в нефтяной и коксохимической промышленности.

Наряду с законами Рауля и Генри в дальнейшем будем пользоваться также и законом Дальтона. Согласно закону Дальтона общее давление газовой (паровой) смеси равно сумме парциальных давлений компонентов:

Р = p₁ + p₂ + p₃ +…+ p_n                          (5)

Одним из важных выводов закона Дальтона является положение о пропорциональности парциальных давлений компонентов идеальной газовой (паровой) смеси и их молярных долей в смеси:

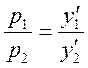
где y¢₁ и у¢₂ — молярные доли компонентов в смеси.

Отсюда следует:

;  

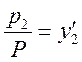
Эти соотношения, справедливые для идеальных газов (паров), позволяют находить состав газа (пара), если известны парциальные давления компонентов. Так как согласно уравнению Рауля p_i = P_i·x'_i  то из предыдущего уравнения следует:

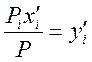
а следовательно,

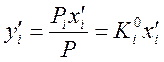                            (6)

где  - константа равновесия;

P_i — давление чистого компонента при заданной температуре;

Р — общее давление паров смеси при той же температуре.

Это уравнение позволяет находить для идеальных систем концентрацию компонента i в паровой фазе, если известна его концентрация в жидкой фазе.

Используя законы Рауля и Дальтона, можно найти равновесные составы жидкой и паровой фаз для идеальных бинарных систем. Для примера рассмотрим систему бензол - толуол.

На рис. 4 изображены две диаграммы, соединенные вместе. На правой диаграмме даны давления паров чистых компонентов как функция температуры. Эта диаграмма строится по экспериментальным данным. Пользуясь построенными кривыми упругости чистых компонентов, в левой части рисунка строим изотермы в координатах с—Р. Изотермы, согласно закону Рауля, являются прямыми линиями. Допустим, что необходимо получить значения равновесных концентраций при давлении 760 мм рт. ст. Проведем в левой части диаграммы горизонталь на уровне 760 мм рт. ст. Для того чтобы найти концентрацию бензола в равновесных парах, если концентрация его в жидкости X' соответствует точке с₁ (см. рис. 4), проведем через точку с₁ вертикальную линию; при этом парциальное давление бензола в смеси будет представлено отрезком ab. Отсюда молярный процент бензола в парах У¢ = 100. Проведя несколько таких построений и расчетов, найдем ряд связанных между собой значений х' и у'. Отложив эти значения в прямоугольных координатах (рис. 5) и соединив их плавной линией, получим линию abc, которая графически изображает связь между содержанием н. к. в паровой и жидкой фазах для постоянного давления.

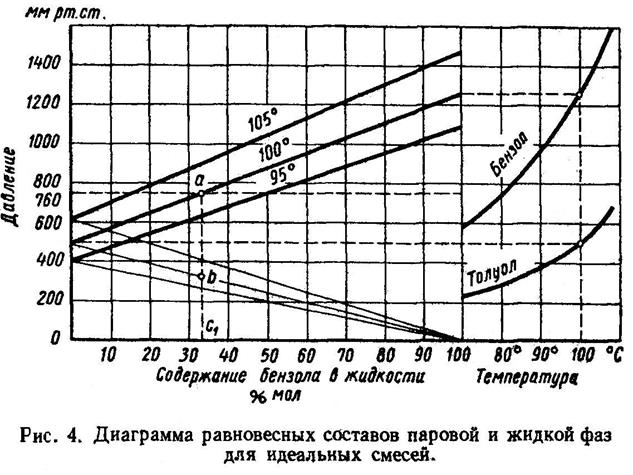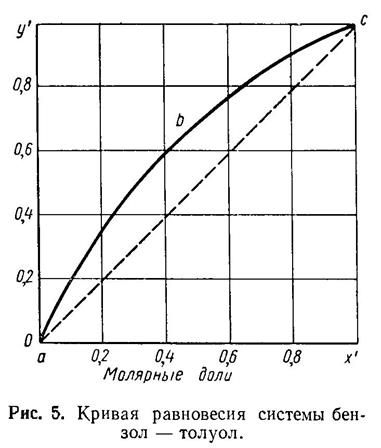Для идеальных смесей содержание компонентов в парах по закону Рауля выражается как:

  и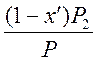 

где x¢ - содержание н. к. в молярных долях;

P₁ и P₂ - упругость пара чистых компонентов при данной температуре;

P - общее давление в системе.

Поэтому:

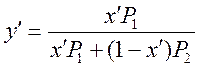                 (7)

Неидеальные системы с полной взаимной растворимостью

Взаимно растворимые неидеальные бинарные системы разделяются на две группы:

а) жидкие смеси, отклоняющиеся от закона Рауля, но не образующие смеси с постоянной температурой кипения;

б) жидкие смеси, отклоняющиеся от закона Рауля и образующие смеси с минимальной или максимальной температурой кипения. Эти смеси носят название азеотропных или нераздельно кипящих смесей.