Исследование оптического спектра газового лазера с помощью сканирующего интерферометра

Лабораторная работа 2

ИССЛЕДОВАНИЕ ОПТИЧЕСКОГО СПЕКТРА ГАЗОВОГО ЛАЗЕРА С ПОМОЩЬЮ СКАНИРУЮЩЕГО ИНТЕРФЕРОМЕТРА

Цель работы – изучение спектральных и пространственных характеристик газового лазера, методики расчета согласования двух оптических резонаторов, приобретение навыков работы с лазером, сканирующим интерферометром, оптическим вентилем.

Предварительные замечания

Генераторы широко применяются в различных электронных приборах. Элементная база этих устройств весьма многообразна, однако общие принципы построения едины для генераторов оптических, микроволновых, радио и низкочастотных колебаний. Все типы генераторов включают в свой состав усилитель и цепь обратной связи. Генерация происходит на частотах, для которых обратная связь положительна, а коэффициент усиления превосходит потери.

В оптическом диапазоне усиление получают за счет инверсии населенности активной среды при ее накачке. Обратная связь осуществляется с помощью зеркал, образующих резонансную систему. В большинстве случаев используются двухзеркальные резонаторы с плоскими или сферическими зеркалами.

Спектральные характеристики лазерного излучения

Параметры линии усиления зависят от природы активной среды. Для используемого в работе He-Ne лазера уширение атомного перехода главным образом определяется эффектом Доплера, вследствие теплового движения атомов. Форма линии усиления (рис. 1) в данном случае описывается функцией Гаусса с шириной по половинному уровню:

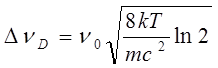                                                 (1)

где ν₀ – центральная частота линии, m – масса атома, k – постоянная Больцмана, T – абсолютная температура (атомная).

Как видно из рис. 1, усиление превосходит потери в полосе частот Δν_Г, однако генерация возможна только для тех частот, для которых выполняется условие положительной обратной связи.

Для лучей, идущих нормально зеркалам это условие определяет, что сдвиг фазы за полный обход резонатора кратен 2π или, что эквивалентно на длине 2d укладывается целое число длин волн:

                                                        (2а)

                                                            (2б)

где d – расстояние между зеркалами резонатора, - волновое число колебаний с длиной волны λ_i, q_i – целое число.

Колебания, для которых справедливы выражения (2) и (3), называются продольными (аксиальными) типами колебаний или продольными (аксиальными) модами.

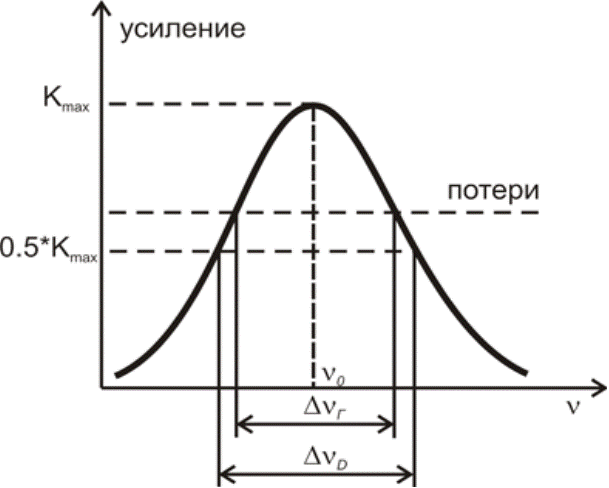               Рис. 1

Легко показать, что частотное расстояние между двумя любыми соседними продольными типами колебаний - Δν_М, называемое межмодовым интервалом, зависит только от расстояния между зеркалами:

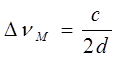                                                          (3)

Соответственно, значения собственных частот аксиальных мод – ν_qопределяется выражением:

                                                         (4)

С учетом сказанного ясно, что спектр генерации в общем случае представляет дискретный набор частот, разделенных интервалом Δν_М. На рис. 2показано увеличение количества мод генерации лазера с ростом усиления активной среды, возникающим при увеличении мощности накачки. При небольшом усилении (кривая 1) генерации нет. В случае 2 генерация происходит только на частоте ν_q, расположенной вблизи центра спектральной линии. Если усиление определяется кривой 3, генерация возникает на трех частотах ν_q, ν_q-1, ν_q+1 и т.д. В этом случае лазер одновременно работает на трех модах.

Аналогичного эффекта изменения числа генерируемых мод можно добиться при постоянной накачке, меняя длину резонатора. Если реализуется условие Δν_Г >> Δν_М, то генерация возникает на многих модах. При противоположном знаке неравенства в пределах линии генерации имеется только один резонанс и генерация осуществляется на одной частоте.

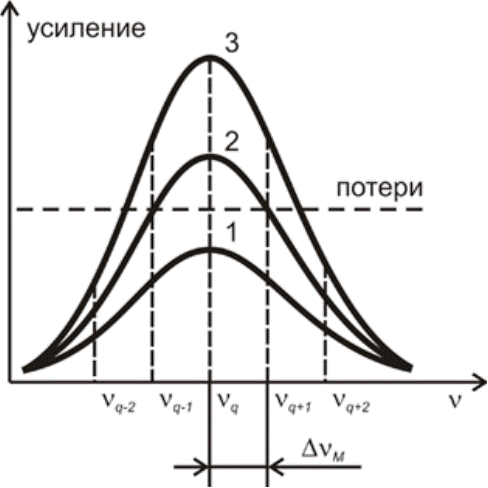                     Рис. 2

Для аксиальных мод распределение поля в поперечной плоскости описывается функцией Гаусса:

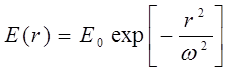                                             (5)

где E₀ – амплитуда поля на оси пучка, , ω – радиус пучка, определенный по уровню 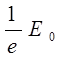 (рис. 3).

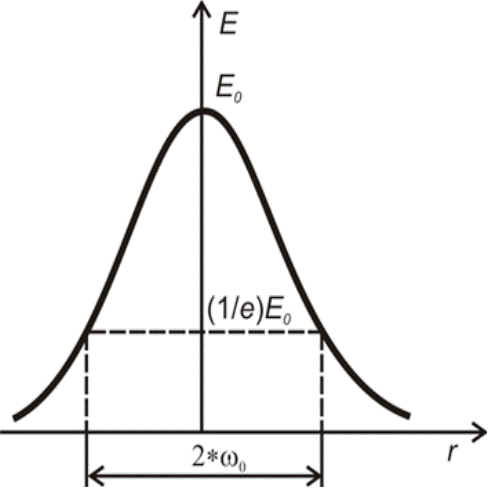                        Рис. 3

Следует отметить, что помимо аксиальных в резонаторе возможны устойчивые типы колебаний для пучков, идущих под определенными небольшими углами к оси резонатора. Такие колебания называются угловыми. Изменение геометрии распространения приводит к различию в спектре частот и характере поперечного распределения поля для наклонных пучков по сравнению с аксиальными. В то же время, радиус кривизны волнового фронта для всех типов волн одинаков в каждом сечении вдоль оси резонатора. На концах резонатора радиус кривизны волнового фронта совпадает с радиусом кривизны поверхностей зеркал.

В связи с тем, что для лазеров обычно используются т.н. открытые резонаторы, без боковых отражателей, высокодобротные колебания не имеют составляющих поля вдоль оси резонатора (оси z, т.е. собственные моды представляют собой поперечные электромагнитные колебания. Они обозначаются как ТЕМ_mnq (transverse electro-magnetic), где m, n и q означают число перемен знака поля по осям x, y и z соответственно. Распределение амплитуды поля вдоль оси резонатора (оси z) имеет вид стоячей волны с узлами на поверхности зеркал.