Распределение энергии в световой волне при различных поперечных модах внутри резонатора легко наблюдать на экране, установленном параллельно зеркалам. Несколько различных мод низкого порядка показано на рис. 4. Над картинами распределения интенсивности приведено распределение амплитуды поля по зеркалу. Распределение амплитуды поля в основной моде ТЕМ00q описывается функцией Гаусса. Моды более высокого порядка описываются полиномами Эрмита, помноженными на функцию Гаусса. Отрицательные величины в распределении амплитуды поля свидетельствуют об обращении фазы. Фаза в модовой конфигурации изменяется на противоположную при переходе от одного пятна к другому.
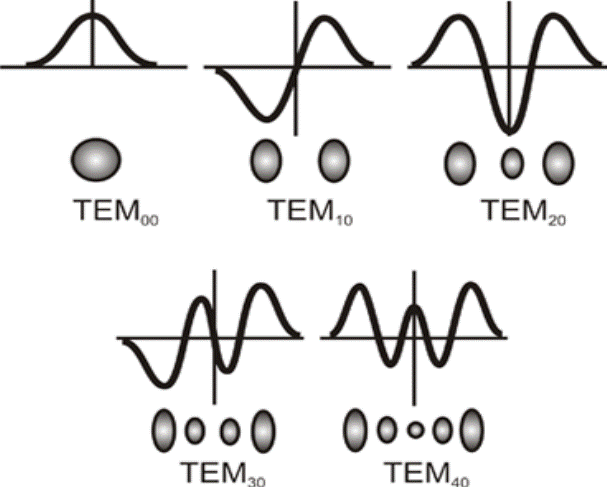Рис. 4
Пространственные характеристики лазерного излучения. Расходимость.
При выходе излучения из лазера и распространении в свободном пространстве меняется как радиус пучка ω, так и кривизна волнового фронта R. Для гауссова пучка справедливы соотношения:
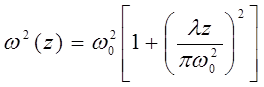(6)
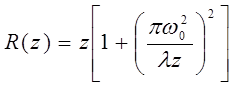(7)
Гауссов пучок имеет минимальный диаметр 2ω0 в «перетяжке» пучка, где волновой фронт плоский.
Гиперболоид 
образует т.н. каустику пучка, в пределах которой
содержится основная энергия волны. Сечение гиперболоида плоскостью, проходящей
через ось z, показано на рис. 5
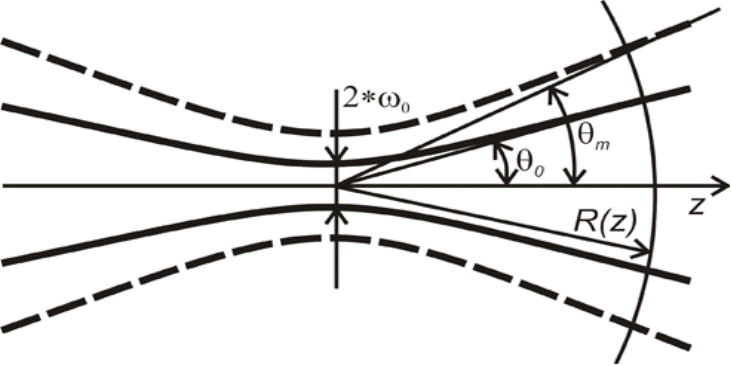
Рис. 5. Сплошной кривой на рисунке изображена каустика ТЕМ00 моды (ω0 – радиус в «перетяжке» пучка, θ0 – расходимость пучка, R(z) – радиус кривизны волнового фронта); пунктиром – каустика высшей поперечной моды с расходимостью θm)
При больших z гиперболоид (6) переходит в конус:
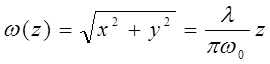(8а)
с половинным углом θ0
при вершине, который принимается за расходимость излучения: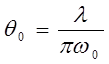 
(8б).
Радиус пучка и расходимость излучения возрастают при увеличении чисел m и n, характеризующих поперечное распределение поля (рис. 4, 5). Расходимость излучения высших поперечных мод θm и θn в плоскостях XOZ и YOZ, соответственно, можно приближенно определить из соотношений:
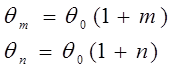(9)
В связи с этим на практике предпочитают реализовывать режим генерации ТЕМ00 моды, которую также называют основной поперечной, нулевой или гауссовой модой.
Сканирующий интерферометр
Для определения спектра непрерывных источников часто используются анализаторы спектра с узкой полосой пропускания, перестраиваемой во времени по длине волны. Такие приборы называются сканирующими (от англ. scan – быстро просматривать). Очевидно, что для адекватного измерения спектра необходимо, чтобы полоса пропускания анализатора была много меньше спектральной ширины изучаемого сигнала. В оптическом диапазоне этому требованию отвечают интерферометры различных типов.
Сканирующие интерферометры широко применяются для исследования спектральных характеристик непрерывных лазеров. Конструктивно прибор представляет собой интерферометр любого типа, одно из зеркал которого можно перемещать в пространстве на расстояние порядка длины волны. С этой целью зеркало устанавливают на пьезоэлемент, к которому прикладывают напряжение требуемой величины с частотой порядка десятков герц.
Отметим, что по терминологии, принятой в радиофизике, такие устройства называются открытыми резонаторами. Интерферометр (резонатор) пропускает излучение на частотах, соответствующих собственным модам резонансной системы. Зависимость коэффициента пропускания интерферометра Т от оптической частоты имеет достаточно слажный характер, определяемый радиусами кривизны зеркал, их коэффициентами отражения и расстоянием между зеркалами (рис, 6а). В случае, если входящий пучок идет строго по оси интерферометра (резонатора), а его пространственные параметры (диаметр и радиус кривизны волнового фронта) совпадают с пространственными параметрами основного типа колебаний резонатора, амплитудно-частотная характеристика принимает вид эквидистантного ряда резонансных кривых (рис. 6), разделенных межмодовым интервалом (постоянная интерферометра) ΔνМ (3). Максимумы пропускания наблюдаются, когда соответствующие длины волн λ, укладываются целое число раз на двойной длине резонатора d, что соответствует условию (2б).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.