Задача № 5
Определить максимальную нагрузку на головку балансира по формулам А.С. Вирновского и А.Н. Адонина и сравнить полученные результаты. Данные для расчета: глубина подвески вставного насоса L, диаметр плунжера насоса Dпл, диаметр насосных труб dт, колонна штанг двухступенчатая – длина штанг верхней ступени dш1 составляет 68%, длина нижней ступени dш2 равна 32%. Длина хода полированного штока S, число качаний в минуту n, плотность жидкости rж = 895 кг/м3.
|
№ |
L, м |
Dпл, мм |
d |
dш1, мм |
dш2, мм |
Тип СК |
S, м |
n |
r, мм |
l, мм |
|
2 |
1270 |
28 |
60 |
19 |
22 |
СК2–0,6–250 |
1,6 |
5 |
295 |
840 |
Решение
Максимальную нагрузку по элементарной (статической) теории определяли по формуле:
![]() = 6863 + 33503 (0,89 + 0,028) = 37619
Н;
= 6863 + 33503 (0,89 + 0,028) = 37619
Н;
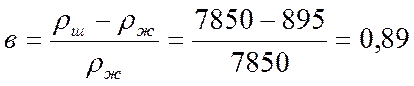 ;
;
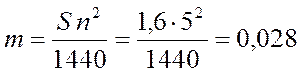 ,
,
где Рж – вес столба жидкости над плунжером, высотой, равной глубине установки насоса L (предусматривается наиболее тяжелый случай, когда динамический уровень находится у приема насоса);
Рш – полный вес насосных штанг;
в – коэффициент потери веса штанг в жидкости;
m – фактор динамичности;
ρш , ρж – соответственно плотность материала штанг и жидкости;
S – длина хода полированного штока;
n – число качаний в мин.
![]() ,
,
где Fпл = 0,78![]() = 0,78 · 28² = 615,5 мм² – площадь
плунжера;
= 0,78 · 28² = 615,5 мм² – площадь
плунжера;
L – глубина установки насоса.
![]() .
.
Максимальную нагрузку на основе динамической теории по формуле А.С.Вирновского с учетом собственных колебаний колонны штанг определяют по формуле:
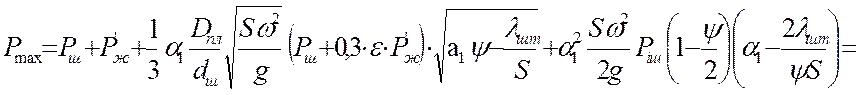
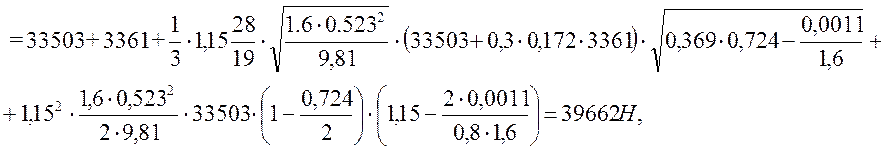 где Рж – вес
столба жидкости между плунжером и штангами:
где Рж – вес
столба жидкости между плунжером и штангами:
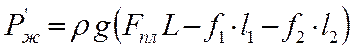 = 895·9,81 (615,5·10
= 895·9,81 (615,5·10![]() ·1270 – 283·10
·1270 – 283·10![]() ·
·1270·0,68 − 380·10
·
·1270·0,68 − 380·10![]() ·1270·0,32) = 3361 Н,
·1270·0,32) = 3361 Н,
f1, f2 = 283·10![]() , 380
, 380![]() –
площади штанг, м²;
–
площади штанг, м²;
S – длина хода точки подвеса штанг (ТПШ);
w – угловая скорость вращения кривошипа:
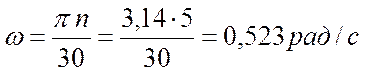 ;
;
ε – отношение площадей просвета:
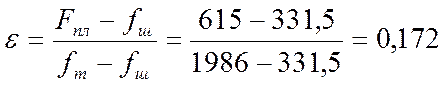 ;
;
fт = 0,785 ∙ d![]() = 0,785
∙ 50,3² = 1986 мм² – площадь проходного сечения трубы, мм²;
= 0,785
∙ 50,3² = 1986 мм² – площадь проходного сечения трубы, мм²;
α1 и а1 – коэффициенты, зависящие от кинематики станка–качалки;
α1=0,5 – коэффициент, равный отношению угла поворота кривошипа π/2 к углу его поворота, при котором скорость достигает максимума;
а1 – кинематический коэффициент:
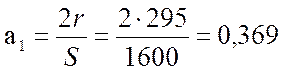 ,
,
где r – радиус кривошипа;
S – длина хода ТПШ;
Ψ – коэффициент:
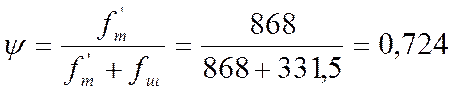 ,
,
где f'т = 868 мм² – площадь сечения труб по металлу;
λшт – удлинение штанг от веса столба жидкости:
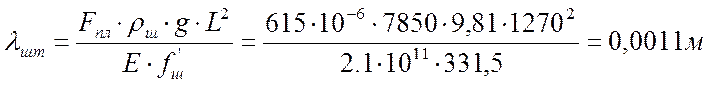 ;
;
ρш – плотность материала штанг;
Е = 2,1·105 МПа – модуль упругости материала штанг;
f'''ш =331,5 мм² – средняя площадь поперечного сечения штанг.
Максимальную нагрузку на основе динамической теории А.Н.Адонина определют по формуле:
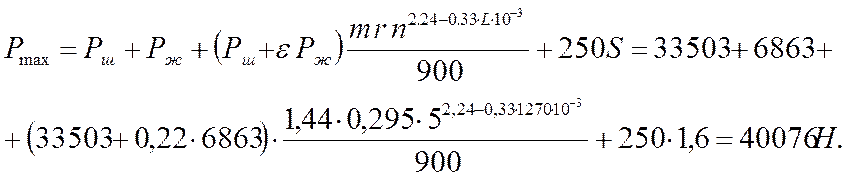
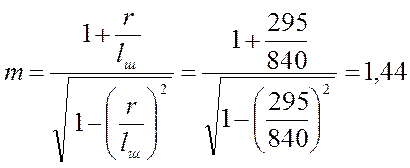 ,
,
где ε – отношение площадей просвета;
т – кинематический коэффициент;
r – радиус кривошипа;
lш – длина шатуна.
Вывод: Исходя из расчетов по различным теориям определения максимальной нагрузки на головку балансира по формулам А.С. Вирновского Рмах=39662 Н и А.Н. Адонина Рмах=40076 Н и по статической теории Рмах=37619 Н - видно различие результатов. Это обьясняется тем , что по статической теории учитываются только статические усилия (вес штанг и жидкости) и максимальное значение сил инерции, а А.С. Вирновский вывел формулу определения Рмах , которая в настоящее время является эталонной и А.Н. Адонин вывел более упрощенную эмпирическую формулу, которая нашла применение в инженерных расчетах.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.