Федеральное агентство по образованию
ГОУ ВПО «Сибирский Государственный индустриальный университет»
Кафедра автоматизированного электропривода и промышленной электроники
Лабораторная работа №1
ВРЕМЕННЫЕ И ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ
ТИПОВЫХ ЗВЕНЬЕВ САУ
Вариант 5
Выполнил: студент гр. АЭП-031
Волынкин Алексей
Проверил: Богдановская Т.В.
г. Новокузнецк
2005 г.
>> W1=tf([50^2],[1 0 50^2])
Transfer function:
2500
----------
s^2 + 2500
>> W2=tf([50^2],[1 2*0.1*50 50^2])
Transfer function:
2500
-----------------
s^2 + 10 s + 2500
>> W3=tf([50^2],[1 2*0.5*50 50^2])
Transfer function:
2500
-----------------
s^2 + 50 s + 2500
>> W4=tf([50^2],[1 2*1.0*50 50^2])
Transfer function:
2500
------------------
s^2 + 100 s + 2500
>> step(W1,W2,W3,W4)
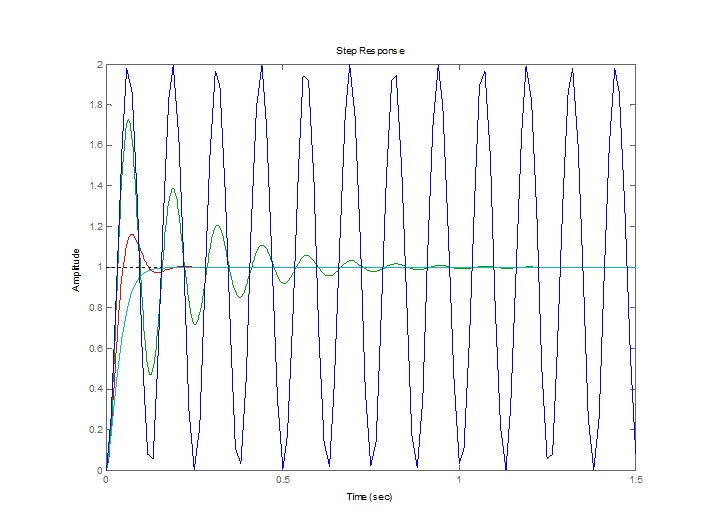
>> impulse(W1,W2,W3,W4)
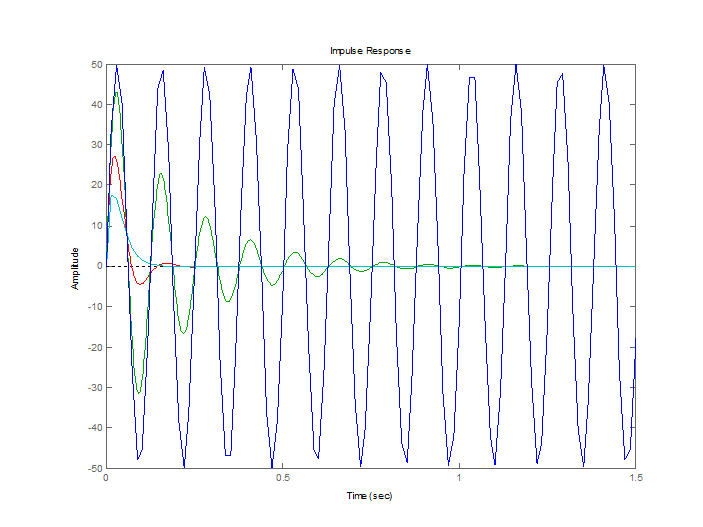
>> [r,p,k]=residue([2500],[1 10 2500])
r =
0 -25.1259i
0 +25.1259i
p =
-5.0000 +49.7494i
-5.0000 -49.7494i
k =
[]
Получим:
-25.1259i 25.1259i
W = ------------------- + -------------------
s + 5.0000-49.7494i s + 5.0000+49.7494i
Отсюда: ![]()
>> nyquist(W1,W2,W3,W4)
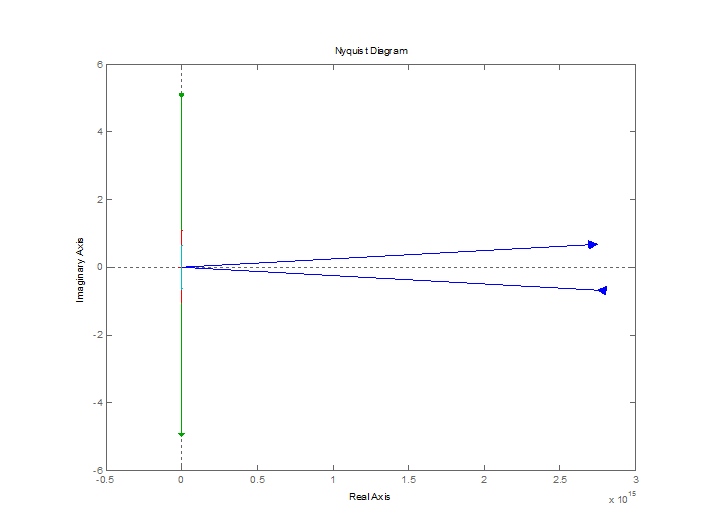
С появлением коэффициента демпфирования годограф Найквиста проходит только по мнимой оси, т.е. исчезает действительная часть. По мере увеличения коэффициента мнимая часть годографа уменьшается, годограф сжимается к началу координат.
>> bode(W1,W2,W3,W4)
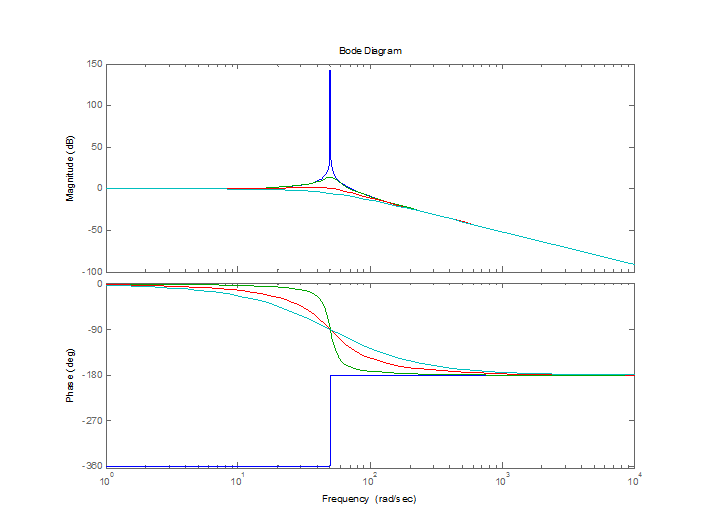
|
Значение |
|
|
W1; |
0…12,4 |
|
W2; |
0…12,3 |
|
W3; |
0…10,1 |
|
W4; |
0…5,07 |
С увеличением коэффициента демпфирования полоса пропускания звена уменьшается.
![]()
![]()
![]()
![]()
>> a = -om*pi*(tan(fi*pi/180) - sec(fi*pi/180));
b = om*pi*(tan(fi*pi/180) + sec(fi*pi/180));
>> W1=tf([1 a],[1 b])
Transfer function:
s + 1436
---------
s + 10.99
>> W2=tf([1 a],[1 b])
Transfer function:
s + 217.7
---------
s + 72.55
>> W3=tf([1 a],[1 b])
Transfer function:
s + 72.55
---------
s + 217.7
>> W4=tf([1 a],[1 b])
Transfer function:
s + 10.99
---------
s + 1436
W1,W4 W2,W3
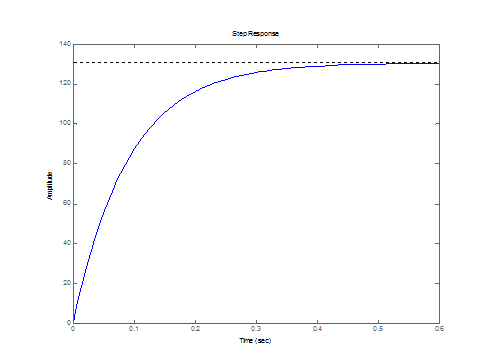
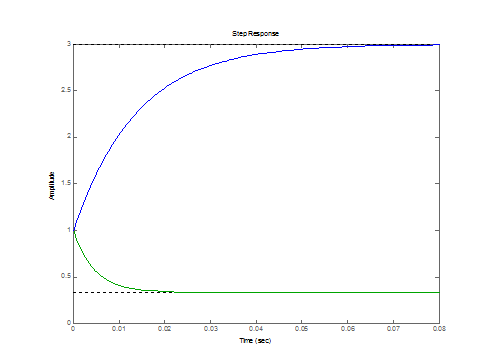 2.3 Найдем аналитические выражения ПХ
2.3 Найдем аналитические выражения ПХС помощью команды residue, а затем воспользовавшись обратным преобразованием Лапласа, получим:
|
W1 |
|
|
W2 |
|
|
W3 |
|
|
W4 |
|
3. Исследование ПИ-регулятора
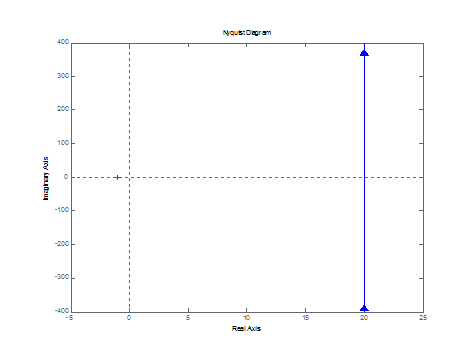
>> W=tf([20*0.05 20],[0.05 0])
Transfer function:
s + 20
------
0.05 s
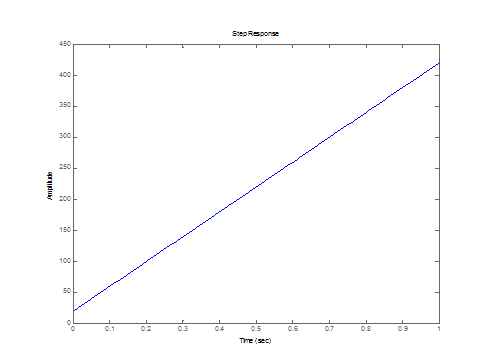 Аналитическое выражение
будет иметь вид
Аналитическое выражение
будет иметь вид ![]()
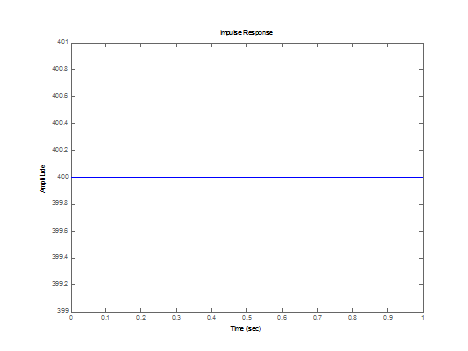 Аналитическое выражение
импульсной характеристики
Аналитическое выражение
импульсной характеристики ![]()
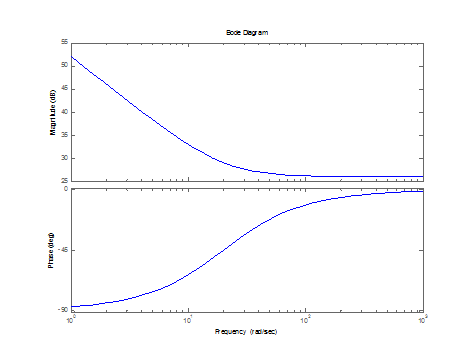
![]() =50;
=50; ![]() =0,05
=0,05
>> W1=tf([150 2*0.05*0.5*50*150 150*(50^2)],[1 2*0.5*50 50^2])
Transfer function:
150 s^2 + 375 s + 375000
------------------------
s^2 + 50 s + 2500
>> W2=tf(1,[1 150])
Transfer function:
1
-------
s + 150
>> W=series(W1,W2)
Transfer function:
150 s^2 + 375 s + 375000
--------------------------------
s^3 + 200 s^2 + 10000 s + 375000
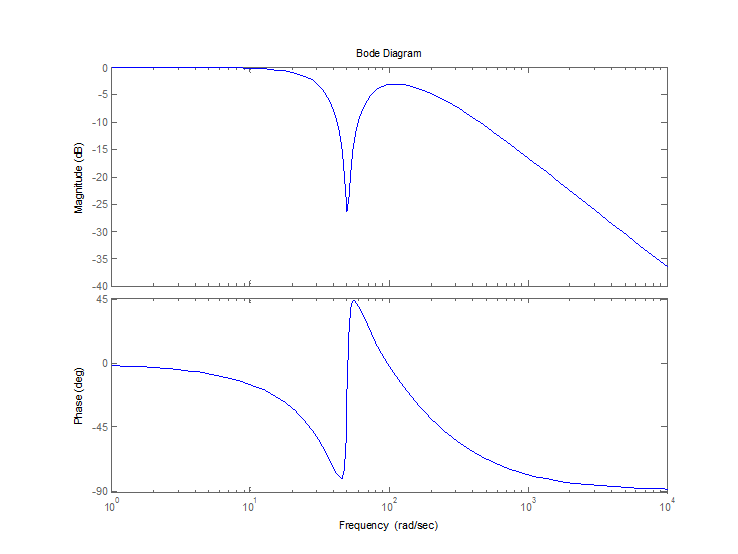
>> om=40
om =40
>> fi=-80
fi =-80
>> a = -om*pi*(tan(fi*pi/180)-sec(fi*pi/180));
b = om*pi*(tan(fi*pi/180) + sec(fi*pi/180));
>> W5=tf([1 -a],[1 b])
Transfer function:
s - 1436
---------
s + 10.99
>> fi=-30
fi =-30
>> a = -om*pi*(tan(fi*pi/180)-sec(fi*pi/180));
b = om*pi*(tan(fi*pi/180) + sec(fi*pi/180));
>> W6=tf([1 -a],[1 b])
Transfer function:
s - 217.7
---------
s + 72.55
>> fi=30
fi =30
>> a = -om*pi*(tan(fi*pi/180)-sec(fi*pi/180));
b = om*pi*(tan(fi*pi/180) + sec(fi*pi/180));
>> W7=tf([1 -a],[1 b])
Transfer function:
s - 72.55
---------
s + 217.7
>> fi=80
fi =80
>> a = -om*pi*(tan(fi*pi/180)-sec(fi*pi/180));
b = om*pi*(tan(fi*pi/180) + sec(fi*pi/180));
>> W8=tf([1 -a],[1 b])
Transfer function:
s - 10.99
---------
s + 1436
>> step(W5,W6,W7,W8)
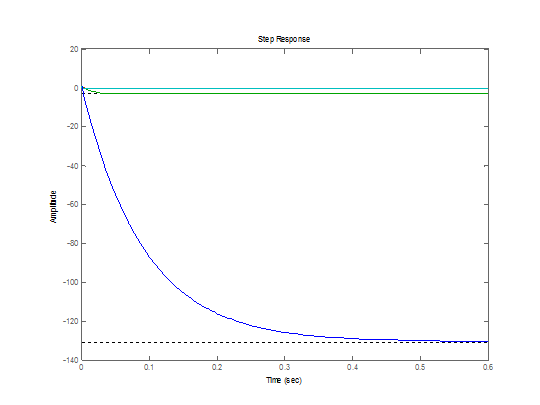
|
W5 |
|
|
W6 |
|
|
W7 |
|
|
W8 |
|
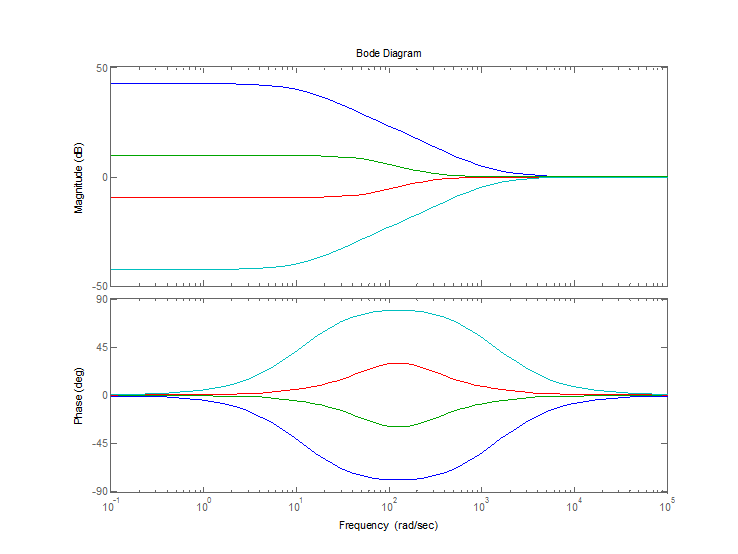
>> bode(W5,W6,W7,W8)
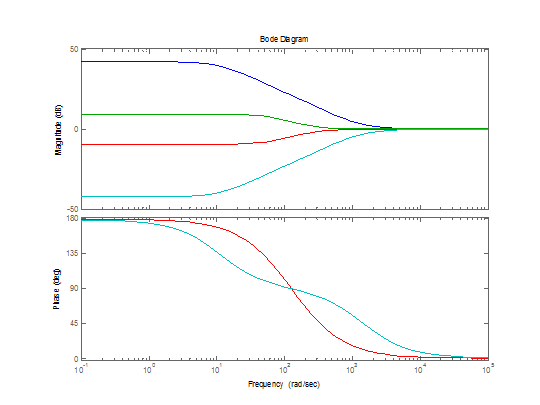
Вывод: проделав лабораторную работу, мы исследовали основные временные и частотные характеристики и соотношения между ними ряда линейных непрерывных звеньев, наиболее часто встречающихся и применяемых в системах автоматического управления.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.