Методические указания к выполнению лабораторных работ в инструментальной среде MatLab по дисциплине «Теория автоматического управления», страница 7

2.2. Краткие теоретические сведения

Как известно, общим условием устойчивости замкнутой системы является нахождение всех корней ее характеристического уравнения в левой полуплоскости плоскости корней. Известно также, что корни, расположенные наиболее близко к мнимой оси, в наибольшей степени влияют на колебательность системы и её запас устойчивости. Расположение корней на комплексной плоскости зависит от структуры и параметров системы, а в частности, от общего коэффициента передачи разомкнутой системы. Все эти положения в настоящей работе проверяются на конкретной системе, заданной передаточной функцией разомкнутой системы. Структура заданной системы такова, что она устойчива лишь в ограниченном диапазоне значений общего коэффициента передачи. При этом уменьшение коэффициента передачи необязательно приводит к увеличению запаса устойчивости, но даже может привести к неустойчивому состоянию. Такой случай соответствует условной устойчивости.

Всe существующие методы оценки устойчивости замкнутых САУ делятся на три группы: корневые методы; алгебраические критерии; частотные критерии. Кгруппе корневых относится непосредственное вычисление корней и построение корневых годографов, и оба эти метода на ПК автоматизированы. Корневые годографы наглядно показывают движение корней замкнутой системы при изменении общего коэффициента передачи ее разомкнутой структуры. К алгебраическим относятся критерии Гурвица и Рауса. Последний более пригоден для реализации на ПК, поэтому он и применяется в работе. При этом определяется диапазон значений коэффициента системы, соответствующий устойчивой работе. Из частотных критериев в работе используется только критерий Найквиста, реализуемый: 1). на плоскости АФХ (прохождение годографа Найквиста относительно критической точки (-l, j0)); на ЛАФЧХ (взаимное расположение точек пересечения ЛАЧХ линии ‘0 дБ’ и ЛФЧХ линии ‘-180 ⁰’).

2.3. Программа работы и порядок её выполнения

2.3.1. Проверка устойчивости замкнутой системы с помощью

общего условия устойчивости и корневого годографа

1.  Ввести в ПК заданную передаточную функцию разомкнутой системы W_i(p) (табл.2.1) как zpk-объект. При этом сначала её нужно привести к виду:

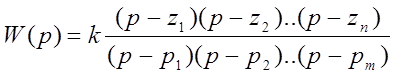
К примеру, нужно задать ПФ 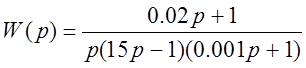. Приводим её к виду zpk-объекта: 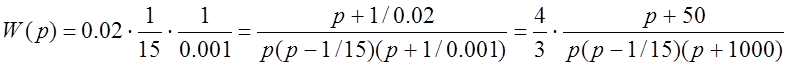. Вводим её параметры как zpk-объекта:

» W=zpk(-50, [0 1/15 1/(-1000)], 4/3)

Zero/pole/gain:

1.3333 (s+50)
s (s-0.06667) (s+1000)

Определить нули и полюсы ПФ командами:

» tzero(W)        -             ищет нули ПФ;

» pole(W)         -             ищет полюсы ПФ;

2.  Ввести ПФ заданной системы, замкнутой обратной связью:

» Wz=feedback (W, 1)

Проверить устойчивость системы, замкнутой обратной связью путем нахождения ее нулей и полюсов. Занести в протокол значения корней замкнутой системы.

3.  Постpoить корневой годограф системы при помощи процедуры pzmap. Если нули и полюса разомкнутой системы сильно разнятся по абсолютной величине, построить годограф раздельно по частным диапазонам величин модулей корней. Для этого после того, как появилась фигура карты корней, воспользуйтесь командой axis, установив границы поля графика в единицах величин, откладываемых по осям:

» axis ([xminxmaxyminymax])                            ,

где     xmin – минимальное значение абсциссы;

xmax – максимальное значение абсциссы;

ymin – минимальное значение ординаты;

ymax – максимальное значение ординаты;

Убедиться, что имеется диапазон значений коэффициента, при которых система будет устойчивой.

4.  С помощью курсора по корневому годографу системы определить диапазон значений коэффициента пepедачи разомкнутой системы, при котором система устойчива в замкнутом состоянии.

2.3.2. Оценка устойчивости по ЛАФЧХ

Построить диаграмму Боде с указанием запасов устойчивости по амплитуде и по фазе командой:

» margin(W)

В интерактивном обозревателе ltiview с помощью курсора найти участок ЛФЧХ, на котором изменением k можно обеспечить устойчивую работу системы. Определить критические значения k. Вывести диаграмму Боде на печать.

2.3.3. Исследование системы при значениях k, близких к критическим