Методические указания к выполнению лабораторных работ в инструментальной среде MatLab по дисциплине «Теория автоматического управления», страница 5

где 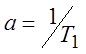,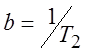(,) – коэффициенты, которые, как и в корректирующем звене с 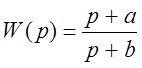, определяют частоту и максимальный фазовый сдвиг, обеспечиваемый звеном. Наличие положительного «нуля» ПФ неминимально-фазового звена обуславливает резкое отличие его фазочастотной xapaктеристики от той же характеристики минимально-фазового звена. В работе, путем снятия частотных характеристик для различных значений  и , изучается расположение ФЧХ неминимально-фазового звена.

1.3. Программа работы и порядок ее выполнения

1.3.1. Исследование звена 2-го порядка

1. Ввести четыре ПФ с именами W1 – W4 позиционного звена второго порядка для заданного  и четырех значений  = 0; 0.1; 0.5; 1.0 (варианты  в таблице 1.1).

2  .С помощью команды

» step (W1, W2, W3, W4)

создать на экране график из четырёх переходных характеристик для этих звеньев.

По указанию преподавателя сделать распечатку графика. С помощью курсора определить перерегулирование для ПФ с  = 0.1 и  = 0.5.

3. По аналогии с предыдущей командой с помощью процедуры impulseсоздать графики из четырёх ИХ для этих звеньев. При соответствующем указании преподавателя вывести график на печать.

4. Получить аналитическое выражение звена при =0.1. Для этого необходимо воспользоваться процедурой residue, которая осуществляет разложение заданной ПФ на простые дроби (см. пример выше). Затем взять обратное преобразование Лапласа с помощью таблицы.

5. Построить в одном графическом окне годографы Найквиста для всех ПФ:

» nyquist (W1, W2, W3, W4)

По согласованию с преподавателем, распечатать график. Сделать заключение о влиянии коэффициента демпфирования на вид годографа Найквиста.

6. С помощью процедуры bodeпостроить график из 4-х ЛАФЧХ (диаграмма Боде) звена для всех значений .

7. Определить значения полосы пропускания звена для всех значений , используемых при выполнении работы. Сделать вывод o влиянии коэффициента демпфирования на пoлocу пропускания звена.

Таблица 1.1

N	1	2	3	4	5	6	7	8	9	10
	10	20	30	40	50	60	70	80	90	100

1.3.2. Исследование корректирующего звена

1. Создать четыре ПФ с именами W1 – W4 для заданного значения частоты и четырёх значений фазы (варианты задания в таблице 1.2).

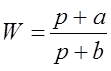        –      ПФ корректирующего звена

Параметры aи b, при которых звено будет изменять фазу на величину  на частоте :

» a = – om*pi*(tan(fi*pi/180) – sec(fi*pi/180))

» b = om*pi*(tan(fi*pi/180) + sec(fi*pi/180))   ,

где     om – заданная частота в Гц;

          fi – угол сдвига фазы в градусах.

2. Построить переходные характеристики звена для 4-х значений фазы. Ввиду большой разницы максимальных значений ПХ их целесообразно строить попарно: W1 и W4 на одном графике, W2 и W3 на другом.

3. Определить аналитические выражения ПХ, используя команду residueи обратное преобразование Лапласа.

4. Построить диаграмму Боде из 4-х ЛАФЧХ для различных ПФ. Построение начать с W1. Затем добавить к ней ЛАФЧХ для W2. После построения двух характеристик провести коррекцию фазы, установив = 0 и ввести графики ЛАФЧХ для W3 и W4. Построенную диаграмму вывести на печать.

Таблица 1.2

N	1	2	3	4	5	6	7	8	9	10
	5	10	20	30	40	50	60	70	80	90

1.3.3. Исследование ПИ-регулятора

1. Ввести ПФ ПИ-регулятора с заданными значениями k_p и Т_р. Варианты заданий в таблице 1.3.

2. Построить ПХ исследуемого звена. Записать аналитическое выражение ПХ, используя процедуру residueи обратное преобразование Лапласа.

3. Построить ИХ ПИ-регулятора и записать её аналитическое выражение.

4. Построить годограф Найквиста. Зафиксировать его форму и параметры в рабочем протоколе.

5. Построить ЛАФЧХ ПИ-регулятора и вывести на принтер.

Таблица 1.3