Расчёт установившихся периодических режимов нелинейной электрической цепи: Методические указания к выполнению расчетно-графической работы, страница 5

После подстановки в полученное выражение для тока (7) закона изменения магнитной индукции в сердечнике (1), в результате математических преобразований получаем выражение для тока в катушке с ферромагнитным сердечником:

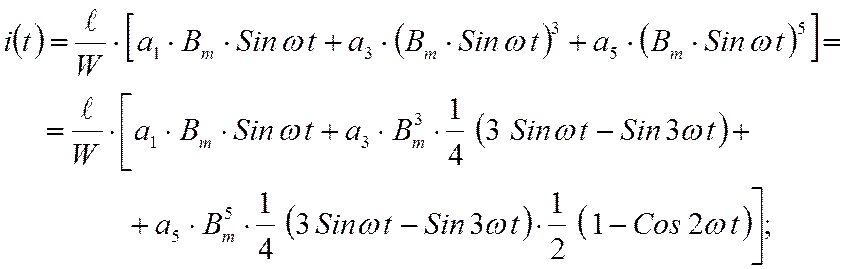
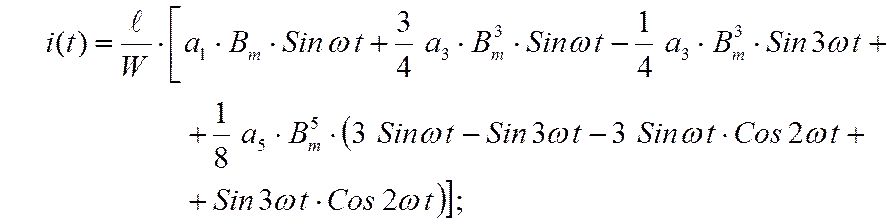
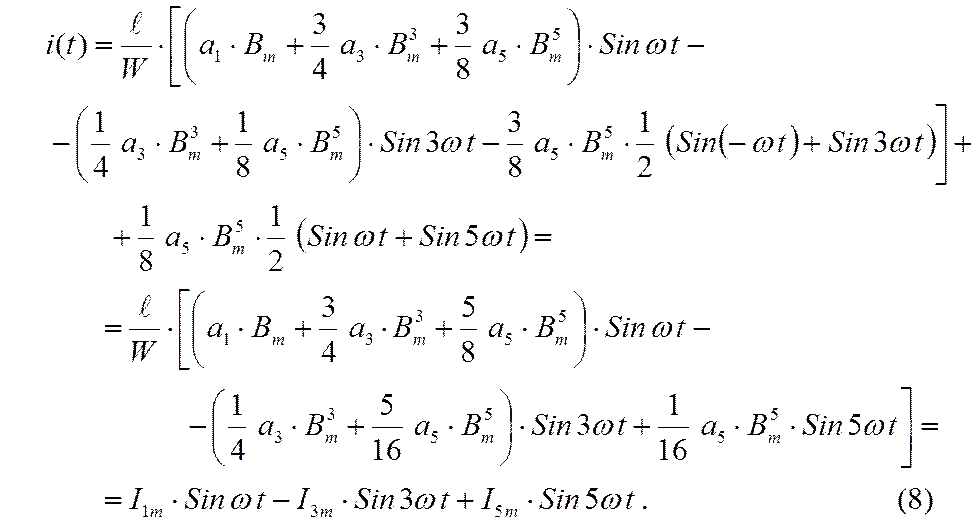
 Ток в катушке с сердечником несинусоидальный (рисунок 4).

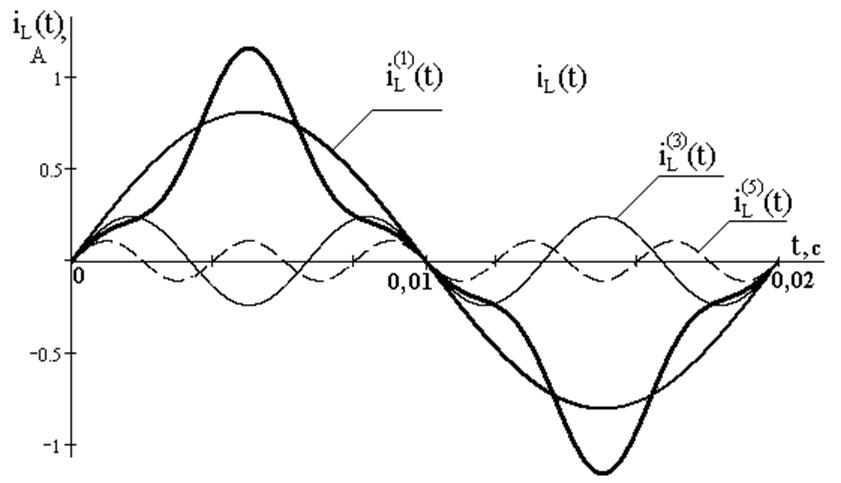
   Рисунок 5 – Закон изменения тока в катушке с сердечником

 Кривая тока в катушке с ферромагнитным сердечником без учёта гистерезиса кривой намагничивания содержит только синусные составляющие нечётных гармоник (симметрия кривой тока    относительно начала координат и относительно оси абсцисс).           В сравнении с синусоидой кривая тока имеет заострённую (пикообразную) форму, так как максимумы составляющих тока 1-й , 3-й  и 5-й гармоник совпадают при 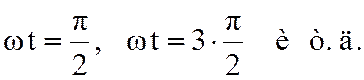                 Следовательно, .

Амплитудные значения составляющих кривой тока в катушке первой, третьей и пятой гармоник определятся:

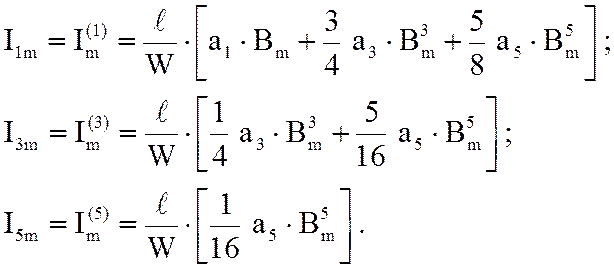                                            (9)

Действующее значение несинусоидального тока в катушке    определится через действующие значения составляющих гармоник:

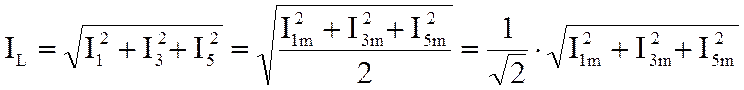       .          (10)

Задаваясь значениями магнитной индукции в рабочем диапазоне , определяем действующее значение напряжения на катушке (формула 3), значения амплитуд гармоник тока (формулы 9), действующее значение тока в катушке (формула 10). Результаты расчёта напряжений и токов  сводим в таблицу 11.

         Таблица 11 – Результаты расчёта ВАХ катушки

Вm , Тл	UL, B	, A	, A	, A	, A
1, 3	…	…	…	…	…
1, 2	…	…	…	…	...
1	…	…	…	…	…
0, 8	…	…	…	…	…
0, 6	…	…	…	…	…
0, 4	…	…	…	…	…
0, 2	…	…	…	…	…

По результатам расчёта режимов для катушки с сердечником (таблица 11) строим вольт-амперную характеристику (ВАХ) катушки с ферромагнитным сердечником .

                  

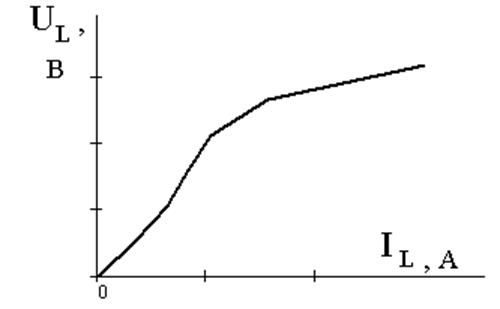
         Рисунок 6 – Вольт-амперная характеристика (ВАХ)

                               катушки с сердечником

Расчёт заданной электрической цепи, содержащей катушку с сердечником и линейные элементы (рисунок 7), выполняем на       основе метода  условной линеаризации (частный случай метода     гармонического баланса).

Метод условной линеаризации заключается в замене фактических несинусоидальных токов и напряжений нелинейной электрической цепи их эквивалентными синусоидами. В основе метода    лежит принцип замены несинусоидальных периодических величин эквивалентными синусоидами, исходя из условия равенства действующих значений несинусоидального тока и напряжения соответственно действующим значениям тока и напряжения эквивалентных синусоид. Кроме того, активная мощность необратимых потерь в катушке, определяемая через несинусоидальные токи и напряжения, должна равняться активной мощности, выраженной с помощью     эквивалентных синусоидальных величин. Период соответствующей эквивалентной синусоиды равен периоду основной гармоники или периоду несинусоидальных кривых тока и напряжения.

Переход к эквивалентным синусоидам тока, напряжения,      магнитного потока и т. д. даёт возможность использовать эффективные частотные методы теории линейных электрических цепей для анализа нелинейных электротехнических устройств, записывать все соотношения в комплексной форме и пользоваться векторными диаграммами.

Метод гармонической (условной) линеаризации рассмотрим на примере электрической цепи, изображённой на рисунке 7. 

                         

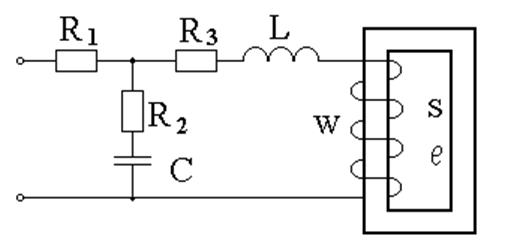
                Рисунок 7  – Заданная электрическая цепь

Реальные кривые напряжения, тока и магнитного потока в     катушке заменяем эквивалентными синусоидами, а индуктивность принимаем условно-нелинейной и зависящей от тока (связь между действующими значениями эквивалентных синусоид тока и напряжения в катушке нелинейная –  таблица 11, рисунок  6).