Расчёт установившихся периодических режимов нелинейной электрической цепи: Методические указания к выполнению расчетно-графической работы, страница 4

Тогда магнитный поток в ферромагнитном сердечнике (магнитопроводе) идеализированной катушки при синусоидальном       приложенном напряжении   определится через ЭДС самоиндукции в катушке:

     

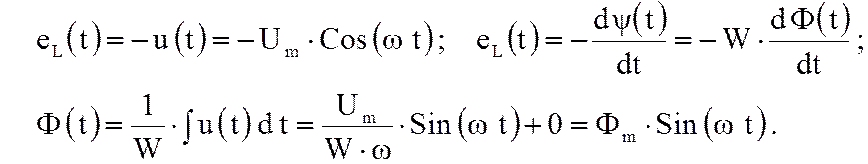
 Здесь:  W – число витков  обмотки,   – угловая частота   источника питания.

Таким образом, при синусоидальном приложенном напряжении магнитный поток в магнитопроводе катушки также синусоидален и отстаёт по фазе от напряжения на угол  .

Значение амплитуды магнитного потока:

                    .  

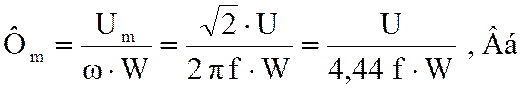Магнитная индукция магнитного поля в сердечнике идеализированной катушки изменяется также по синусоидальному закону:

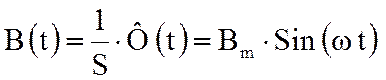                                      .                                (1)

Значение амплитуды магнитной индукции:

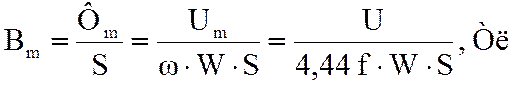                        .                   (2)

Действующее значение приложенного к катушке напряжения связано с амплитудой магнитного потока (амплитудой магнитной индукции) в сердечнике соотношением:

            .                       (3)

Закон изменения тока в катушке определим графо-аналитическим методом с помощью аппроксимирующего выражения для кривой намагничивания материала сердечника. Полагаем, что магнитопровод катушки выполнен из магнитно-мягкой стали с малыми потерями, для которой петлёй гистерезиса можно пренебречь и считать зависимость   или  (кривую намагничивания материала сердечника) однозначной.

Аппроксимирующее выражение для кривой намагничивания материала сердечника примем в виде степенного полинома:

                             .                                      (4)

Коэффициенты аппроксимирующего полинома  для заданного сердечника катушки определятся методом выбранных точек на основании заданной кривой намагничивания материала сердечника (таблицы 3  10). Выбираем в рабочем диапазоне  характеристики (рисунок 3) три расчётные точки А₁, А₂, А₃ (предварительно разбив рабочий диапазон на четыре примерно равные области) с координатами:

                               .

                               

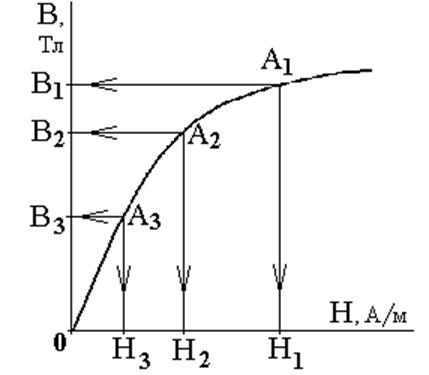
Рисунок 3 – Определение коэффициентов аппроксимирующего   полинома заданной кривой намагничивания

Для определения коэффициентов аппроксимирующего выражения  заданной кривой намагничивания сердечника катушки получаем систему трёх уравнений: 

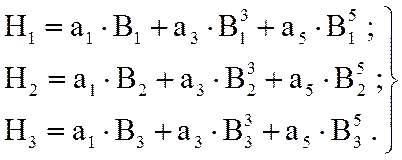                                                            (5)

Решение системы уравнений (5) определит коэффициенты         аппроксимирующего полинома (4) заданной кривой намагничивания материала сердечника: .

С помощью программы компьютерной математики MathCad      коэффициенты аппроксимирующего полинома кривой намагничивания сердечника определятся:

  ;        ;          ;         .

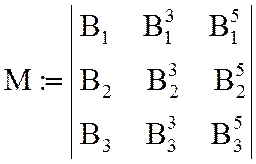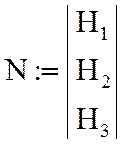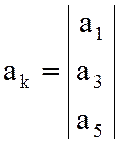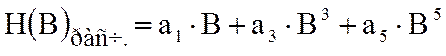                     .                                (6)

Заданная (табличная) и расчётная кривые намагничивания сердечника катушки приведены на рисунке 4.

                                  

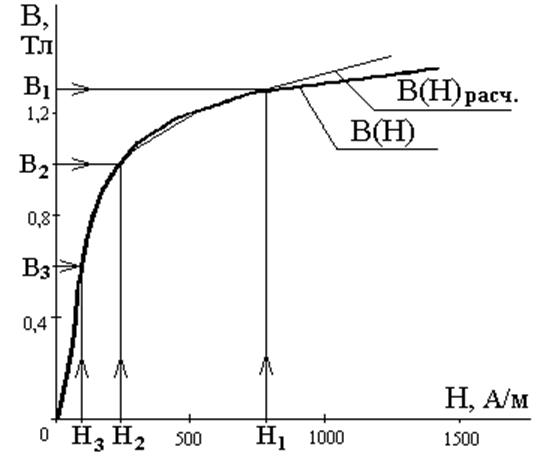
           Рисунок 4 – Заданная (табличная) и расчётная кривые

                                 намагничивания сердечника катушки

Связь между током в катушке и напряженностью магнитного поля в сердечнике определится на основании второго закона Кирхгофа для магнитной цепи. Для идеализированной катушки с однородной магнитной цепью имеем один участок разбиения:

                                     .

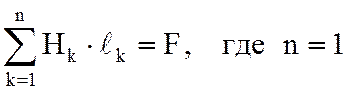Магнитодвижущая сила катушки (МДС)  с числом витков     обмотки  и током   определится:

                                         .

 Уравнение связи между током в катушке и магнитной индукцией магнитного поля в сердечнике с учётом аппроксимирующего выражения кривой намагничивания сердечника (4) запишется:

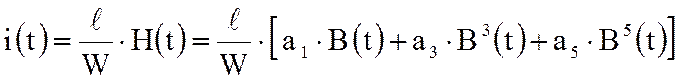            .              (7)

       Здесь:  W – число витков обмотки;  – длина средней магнит    ной  силовой линии магнитопровода катушки.

Магнитная индукция в сердечнике катушки изменяется по     синусоидальному закону (1, 2).

Закон изменения тока в катушке со стальным сердечником     определится на основании выражения (7) и закона изменения       магнитной индукции в сердечнике при заданном входном напряжении (1, 2).