Информационные технологии управления: Задания и методические указания для выполнения курсовой работы, страница 8

=$E$4*$E$11*10-B4 = 4,0

Ø доход предприятия при низком спросе на продукцию

Ø =$E$5*$E$12*10- B4 = -2,1

Ø =средняя доходность предприятия

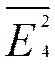 =СРЗНАЧ(G9:H9)= 0,95

      среднее квадратичное отклонение значения прибыли при тех же условиях составит:

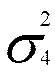  =СТАНДОТКЛОН(G9;H9)= 4,31

Ø величина риска ошибки

Ø 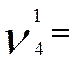  ç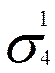 / 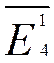ç = =ABS(J9/I9)= 4,54

2.         "Ветвь" строительства небольшого предприятия ( с возможностью реконструкции):

2.1. реконструкция предприятия

Ø доход предприятия при высоком спросе на продукцию

=($E$8*$E$11*8-$C$8)+($E$8*$E$11*2-$B$8)= 4,8

Ø доход предприятия при низком спросе на продукцию

=($E$9*$E$12*8-$C$8)+($E$9*$E$12*2-$B$8)= -0,90

Ø средняя доходность предприятия

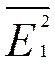 =СРЗНАЧ(G10:H10) = 1,95

Ø среднее квадратичное отклонение значения прибыли составит

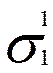 = =СТАНДОТКЛОН(G10:H10) = 4,03

Ø величина риска ошибки

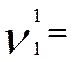  ç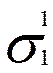 /  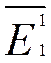 ç =ABS(J10/I10)= 2,07

2.2. без реконструкции

Ø доход предприятия при высоком спросе на продукцию

=($E$6*$E$11*8-C6)+($E$6*$E$11*2-B6) = 0,75

Ø доход предприятия при низком спросе на продукцию

=($E$7*$E$12*8-$C$6)+($E$7*$E$12*2-$B$6) = -0,4

Ø средняя доходность предприятия

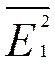  =СРЗНАЧ(G11:H11)= 0,18

Ø величина риска ошибки

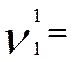  ç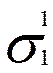 /  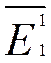 ç   =ABS(J11/I11)= 1,09

3.  "Ветвь" строительства небольшого предприятия:

Ø доход предприятия при высоком спросе на продукцию

= $E$10*$E$11*10-$B$10= 1,15

Ø доход предприятия при низком спросе на продукцию

= $E$10*$E$12*10-$B$10= 0,15                      

Ø средняя доходность предприятия

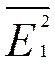= =СРЗНАЧ(G12:H12)= 0,65

Ø среднее квадратичное отклонение значения прибыли при тех же условиях составит:

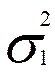 =СТАНДОТКЛОН(G12:H12)= 0.71

Ø величина риска ошибки (при тех же условиях) может быть определена как:

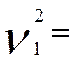  ç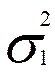/  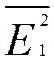ç= =ABS(J12/I12) =1,09

Вывод

Анализ результатов расчетов, выполненных для  "узла решений" 1 показывают, что максимальная прибыль предприятия (1,95 тыс. у.е) за 10-ти летний период работы может быть получена при строительстве небольшого предприятия с реконструкцией его при условии, что в течение первых 2-х лет его работы будет наблюдаться высокий уровень спроса. Величина риска, при этом, составит 2,07

Окончательно принимаемое решение зависит от индиви­дуального отношения ЛПР к величине реальных значений проигрыша или выигрыша и желания рисковать ради получения выигрыша.

2.3  Анализ полученного решения методом имитационного моделирования

,  При решении предыдущей части примера мы полагали, что вероятность высокого (или низкого) спроса на продукцию постоянна в течение всего времени работы предприятия. В действительности вероятность уровня спроса на продукцию определенного вида подвержена колебаниям (например, сезонным).

В простейшем случае учет влияния непостоянства спроса на деятельность предприятия может быть решен построением модели со случайным изменением уровня спроса.

В соответствии с заданием будем считать, что  вероятность спроса на изделия подчинена равномерному закону распределения в интервале [-25%, 25%] от величины указанной в задании (строки 11 -12 таблицы 2-2.). Т.е для условий примера значение вероятности уровня высокого спроса (ячейка Е11) может принимать случайные значения в диапазоне от 0,45 до 0,75.

Построение модели

Скопируйте решенную задачу на отдельный лист Excel, присвоив ему имя «Имитация»

Для решения задачи используем метод имитационного моделирования с использованием датчика случайных чисел (метод Монте –Карло) и процедуру «Описательная статистика»  (СЕРВИС_АНАЛИЗ ДАННЫХ… _Описательная статистика).

Пояснения.

  Имитационное моделирование с применением функции =СЛЧИС() ППП EXCEL