Информатика и выч. техника \ Информационные технологии управления

Информационные технологии управления: Задания и методические указания для выполнения курсовой работы, страница 7

 Ко­личественные оценки последствий всех возможных вариантов реше­ний (в у. е.) взяты из таблицы 2-3 (столбец "Годовой доход (Прим)".)

Анализ "дерева" выбора решения проводится справа налево (в направлении, "обрат­ном" течению времени).

В каждом "узле решения" производится::

Ø  расчет значений целевой функции используемого критерия - средней величины прибыли предприятия за соответствующее количество лет (поэтапно для каждо­го варианта решения, которое может быть принято в этом узле).

Ø  Расчет относительной ве­личины риска ошибки, определяемой по  значению коэффициента вариации.

Оконча­тельное решение в "узле" принимается на основе совместного анализа полученных численных результатов величины выигрыша (или проиг­рыша) и риска ошибки при оценке их величины.


 


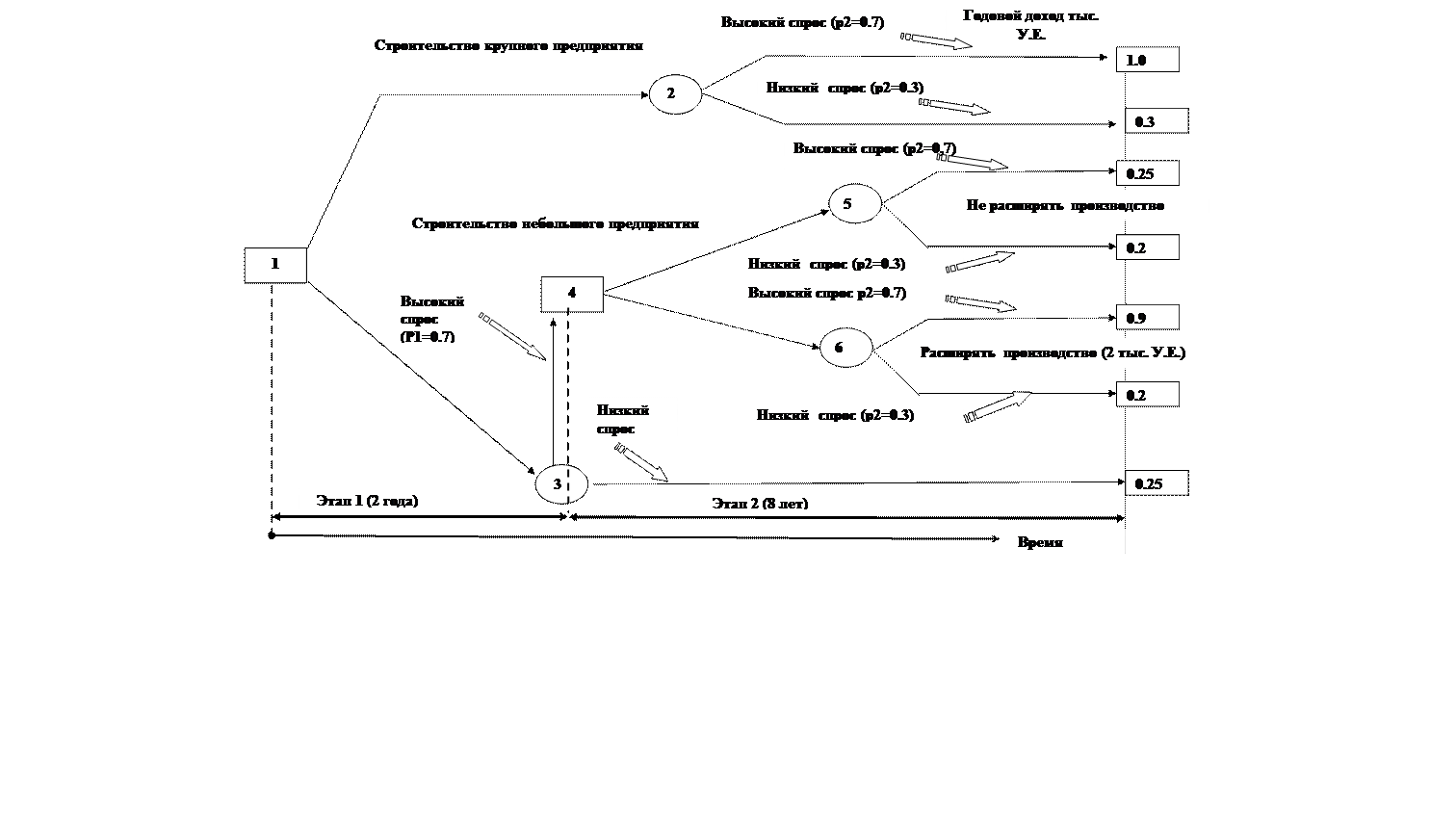Рис. 1  "Дерево решений" с данными примера

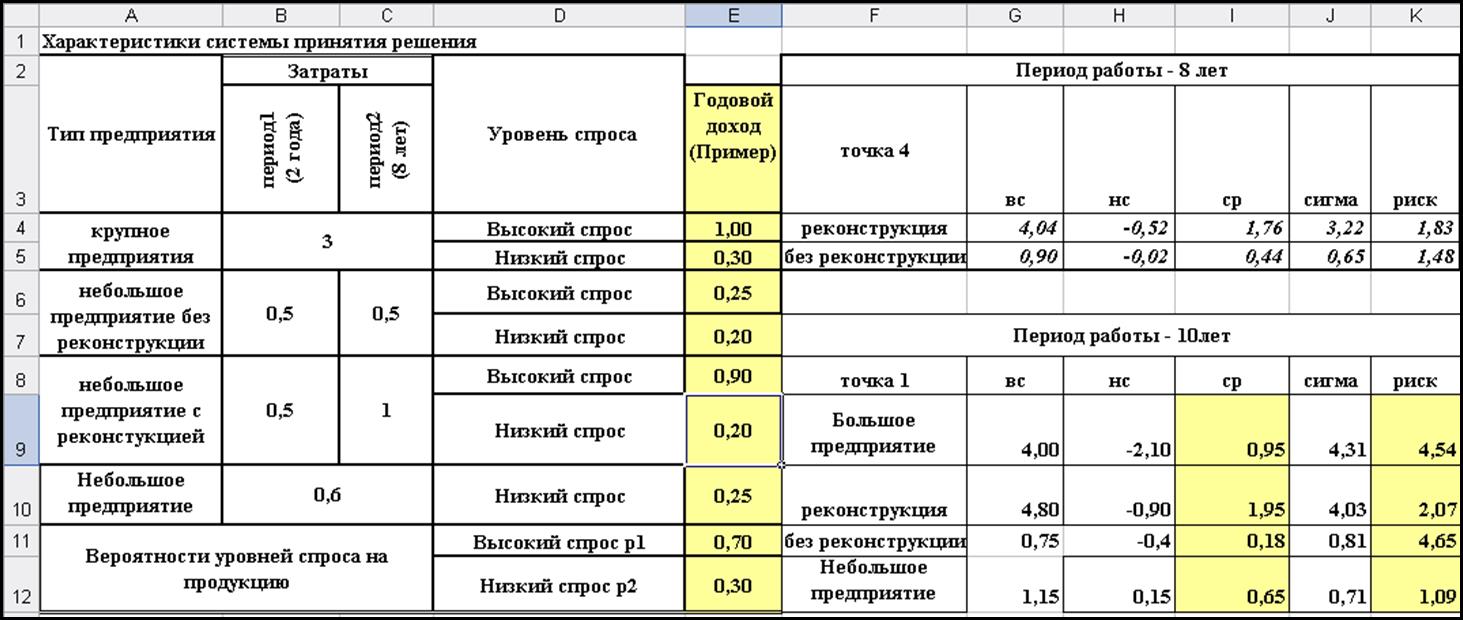
Рис. 2.Фрагмент листа Excel c исходными данными примера и его решением.

Обозначения заголовков:

вс – высокий спрос;

нс – низкий спрос;

сигма – среднеквадратическое  отклонение дохода предприятия;

риск – коэффициент риска

 



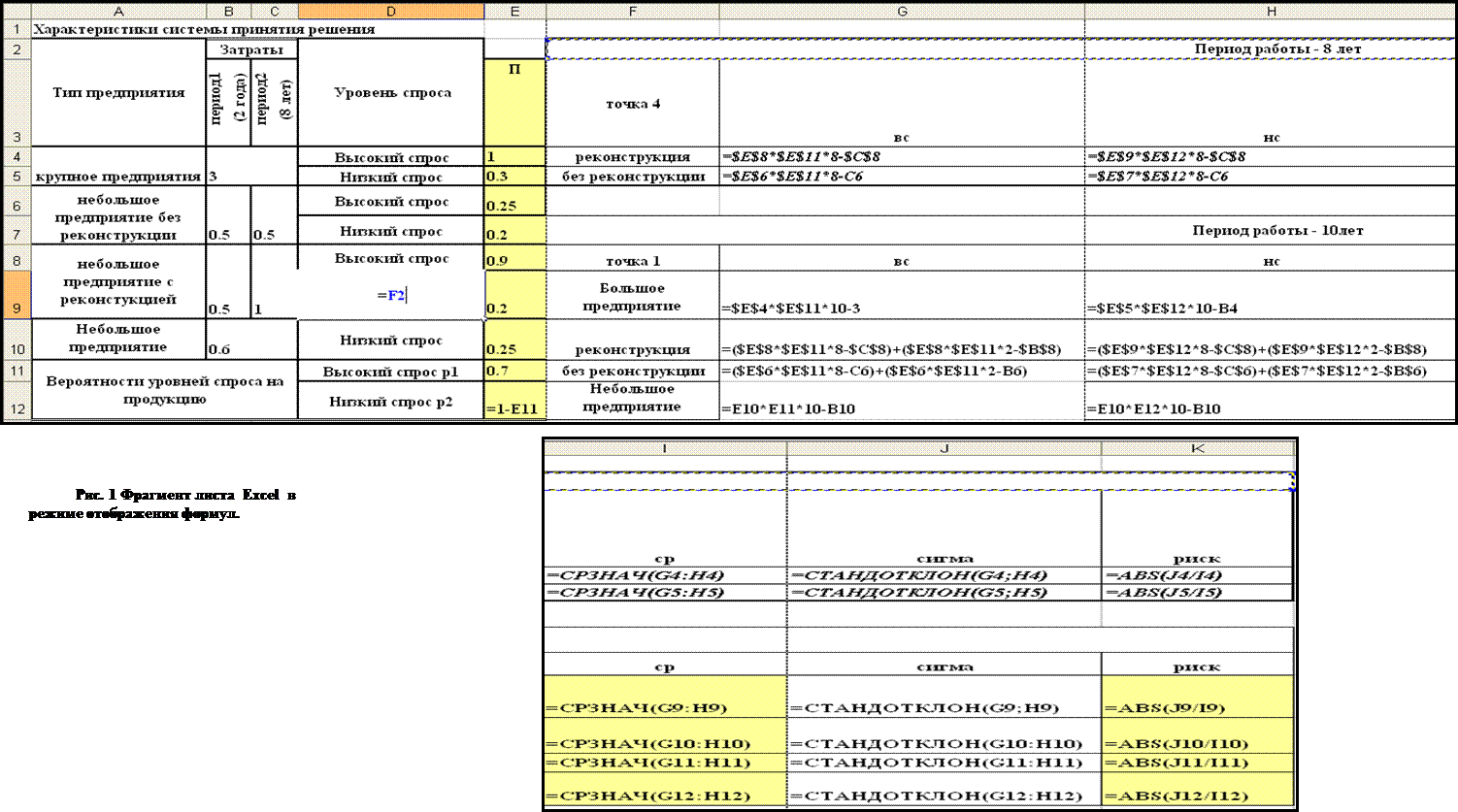Как следует из приведенного рисунка, на "дереве" имеется два "узла решения" с номерами 1 и 4. Первым справа расположен "узел" 4, который по указанным выше со­ображениям анализируется первым.

Расчет "узла решений" 4

1. "Ветвь" реконструкциии (расширения) небольшого предприятия:

Расчеты представим в таблице, подобной приведенной на рисунке 2-1.

Ø значение прибыли небольшого предприятия за 8 лет (по уровню спроса ) может быть определено как  среднее значение ожидаемой годовой прибыли с учетом вероятности ее получения умноженное на период анализа (8 лет) за вычетом суммы, затрачиваемой на расширение производства:

Ø В ячейках G4:K4 вычислим характеристики доходности предприятия при проведении его реконструкции (расширения)

o  в ячейке G4 вычислим доход предприятия при высоком спросе на продукцию  $E$8*$E$11*8-$C$8= 4,04

o  в ячейке H4 вычислим доход предприятия при низком спросе на продукцию =$E$9*$E$12*8-$C$8= - 0,52

o  в ячейке I4 вычислим среднюю доходность предприятия

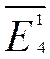 = СРЗНАЧ(G4:H4)=1.76

Ø среднее квадратичное отклонение значения прибыли, рассчитанное в ячейке   J4   составит:

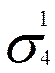 =СТАНДОТКЛОН(G4;H4) =3,22

Ø величина риска ошибки (при тех же условиях) может быть определена как (ячейка K4):

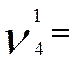  ½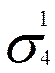 / 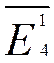½ = =ABS(J4/I4)= 1.83

2. "Ветвь «без реконструкции небольшого предприятия:

Ø доход предприятия при высоком спросе на продукцию

 =$E$6*$E$11*8-C6=0,9;

Ø доход предприятия при низком спросе на продукцию

=$E$7*$E$12*8-C6 = -0,02

Ø средняя доходность предприятия

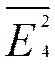 =СРЗНАЧ(G5:H5) = 0,44

      среднее квадратичное отклонение значения прибыли при тех же условиях составит:

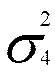 =СТАНДОТКЛОН(G5;H5) = 0,65

Ø величина риска ошибки

Ø 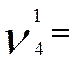ç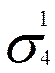 / 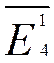ç ==ABS(J5/I5)= 1,48

Сравнивая полученные результаты, можно сделать следующий вы­вод: при расширении небольшого предприятия есть шанс получить сред­нюю прибыль в размере    3, 22 тыс. У. Е., а при условии его не расширения  1,48 тыс. У. Е. Таким образом, в последнем случае (т. е. в случае принятия в "узле" 4 решения " расширять" производство) средняя ожидаемая прибыль пред­приятия за 8 лет в 3,22/1,48 = 2,17 раза выше, чем в случае принятия альтернативного решения. При этом риск возможной ошибки при оценке величины средней прибыли в случае принятия решения о расширении производства оказывается в 1,83/1,48= 1,23 раза выше.

Расчет "узла решений" 1

1.         "Ветвь" строительства крупного предприятия:

Ø доход предприятия при высоком спросе на продукцию

Скачать файл