Лекции по высшей математике.
Понятие системы координат на плоскости. Декартовы координаты.
Порядок построения:
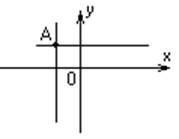 Плоскость покрывается бесконечной сеткой взаимно
перпендикулярно прямых параллельно осям.
Плоскость покрывается бесконечной сеткой взаимно
перпендикулярно прямых параллельно осям.В результате любая точка плоскости располагается на пересечении какой-то пары прямых сетки.
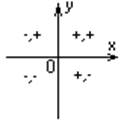 Опускаем перпендикуляры из точки на координатные
оси и измеряем длины отрезков от точки пересечения до начала координат.
Опускаем перпендикуляры из точки на координатные
оси и измеряем длины отрезков от точки пересечения до начала координат.Полярные координаты.
Порядок построения:
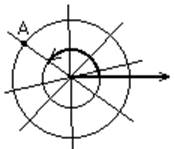 Из точки во все стороны проводятся лучи.
Из точки во все стороны проводятся лучи. В результате любая точка плоскости лежит на пересечении какой-то окружности и луча.
Формулы связи между полярными и декартовыми координатами.
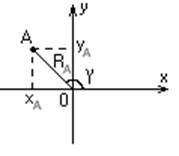
![]() ,
,
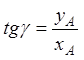 ,
угол доопределяется с учетом четверти.
,
угол доопределяется с учетом четверти.
![]() ,
,
![]()
Понятие о декартовых координатах в пространстве.
Порядок построения:
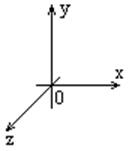 Через начало координат проводится три взаимно
перпендикулярных прямых.
Через начало координат проводится три взаимно
перпендикулярных прямых.В результате каждая точка в пространстве пересечена тремя плоскостями.
Декартовыми координатами точки в пространстве называются длины отрезков (с учетом знаков) отсекаемых на координатных осях плоскостями.
Задание точек при помощи радиус-векторов.
Порядок построения:
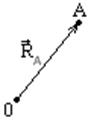 Выбирается начало
координат.
Выбирается начало
координат.![]() -
радиус-вектор точки A.
-
радиус-вектор точки A.
Сложение векторов.
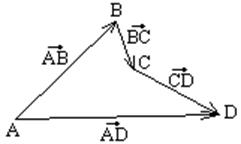 Сумма векторов – направленное перемещение из начальной точки в
конечную.
Сумма векторов – направленное перемещение из начальной точки в
конечную.
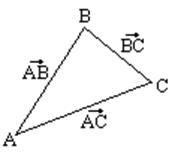
![]()
Главное научиться складывать два вектора.
Из
правила сложения векторов следует правило вычитания: ![]() .
.
Действия сложения, вычитания и растяжения вектора, умножение на константу называют единым словом – линейные операции над векторами.
Взаимосвязь задания точек.
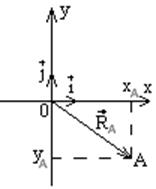 Хотим, чтобы RA было суммой двух векторов параллельно координатным осям. Длины
слагаемых – модуль координат. Чтобы определить направление с координатными
осями связывают пару векторов вдоль положительных направлений осей.
Хотим, чтобы RA было суммой двух векторов параллельно координатным осям. Длины
слагаемых – модуль координат. Чтобы определить направление с координатными
осями связывают пару векторов вдоль положительных направлений осей.
![]() .
.
Когда речь идет о точках в пространстве в сумму добавляется еще один вектор:
![]() .
.
Все действия сложения, вычитания и умножения на числа выполняются при помощи группировки и приведения подобных.
Лекция №2. Анализ функции одной переменной. (7.09.00)
Основные обозначения.
Ниже будут рассматриваться функции задаваемые формулами.
Область определения функции (D(f)) – множество значений переменных при которых формула функции не противоречива. D(y) находится способом взятия всех чисел и выбрасыванием всех которые приводят к противоречию функции.
Область значений функции (E(f)) – множество чисел, которое образует значение функции когда переменная пробегает всю D(f).
График функции (G(f)) – множество пар (x, f(x)) при xÎD(f). Пример: G(f)={(x, f(x)):xÎD(f)}.
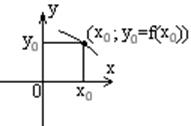 График удобно
интерпретировать как множество точек на координатной плоскости.
График удобно
интерпретировать как множество точек на координатной плоскости.
 По графику удобно
классифицировать функции. Если график функции представляет из себя единую
линию, функцию называют непрерывной.
По графику удобно
классифицировать функции. Если график функции представляет из себя единую
линию, функцию называют непрерывной.
 Из одного значения
функции можно получить другое её значение, изменяя значение переменной и не
сходя с графика функции. Эта процедура описывается символом предельного перехода:
Из одного значения
функции можно получить другое её значение, изменяя значение переменной и не
сходя с графика функции. Эта процедура описывается символом предельного перехода:
![]() .
.
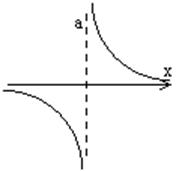
Функции не являющиеся
непрерывными являются разрывными. Простейший пример: 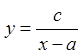 ; с>0.
; с>0.
При работе с разрывными
функциями процедура предельного перехода возможна не всегда. Предельный переход
![]() может
быть выполнен только тогда, когда интервал не содержит точек разрыва функции.
может
быть выполнен только тогда, когда интервал не содержит точек разрыва функции.
Кроме описанных разновидностей функций бывают функции на дискретное множество точек. Графики таких функций – несвязные точки на плоскости.
Функции, бесконечно большие и бесконечно малые.
Понятие бесконечно большой и бесконечно малой используются для локального описания поведения функции. Локальная – вблизи выбранной точки.
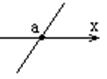 Пример:
Пример: ![]() .
.
Определение бесконечно
малой функции ![]() .
.
Функция называется бесконечно малой вблизи точки a, если ее значение стремится к 0, когда x®a.
Тоже самое пишут при помощи
символа предела: ![]() .
.
Бесконечно большая функция
![]() .
.
Функция называется бесконечно большой в точке b, если ее значение по модулю неограниченно растут, когда переменная приближается к b.
Тоже самое пишут коротко
при помощи символа предельного перехода: ![]() .
.
Пример: Dxa=x-a является бесконечно малой при x®a и бесконечно большой при x®+¥ или x®-¥.
Взаимосвязь между бесконечно большими и бесконечно малыми функциями.
Деление постоянной на бесконечно малюю дает бесконечно большую и наоборот деление постоянной на бесконечно большую дает бесконечно малую.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.