Векторная алгебра. Анализ функции одной переменной. Равенства векторов и разновидность векторов. Дифференцируемая функция. Вычисление расстояния от точки до прямой, страница 5

  Если прямые пересекаются, то угол между ними находится как угол между  и  при помощи формул скалярных произведений, а точка пересечения как решение системы уравнений.

Лекция №6. Дифференциал и геометрический смысл дифференцирования. (21.09.00)

  Дифференциал – линейная часть приращения дифференцированной функции.

              Обозначение. .

  Согласованно с этим определением  обозначает , т.е. . От этой записи и пошло Лейбницево обозначение производной .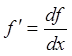

  Геометрический смысл дифференцирования состоит в том, что данная операция сопоставляет точке графика касательную, там где производная существует, для этого пишут формулу: .

  Перепишем это уравнение в следующую формулу: 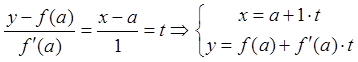 - это уравнение прямой линии, которая проходит через точку  вдоль вектора .

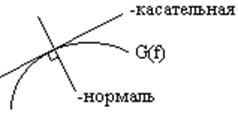
  В данной конструкции касательный вектор  определен в каждой точке, где функция имеет производную. Зная этот вектор легко написать уравнение прямой линии, которое является касательной к графику. Если уравнение касательной записать в форме общего уравнения: , то из него можно прочитать вектор, который направлен вдоль прямой, перпендикулярной к касательной: . Прямая проходящая через точку вектора  перпендикулярная ему называется нормаль (рис).

Дифференциал в приближенных вычислениях.

  Дифференциал предоставляет возможность подсчитать значение функции по известному опорному значению:

 . Например:

  , a=25, , .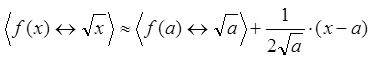

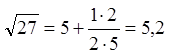Производная в физических приложениях.

  Производной характеризуют скорость изменения разнообразных физических величин (необязательно во времени).

  Примеры. 

             

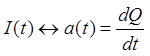
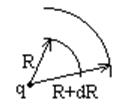
Приближение дифференцируемой функции многочлена.

Теорема Тейлора.

Производные внешних порядков.

  Операция дифференцирования сопоставляет функцию и ее производную. К этой функции (производной) также можно применить операцию дифференцирования. Функция полученная из исходной двумя дифференцированиями называется второй производной и обозначается:  или .

  Процесс дифференцирования можно продолжить и дальше. Производная функции  порядка n обозначается , эта функция получена из  n-кратных раз дифференцирования.

Формула Тейлора.

  Формула Тейлора уточняет что стоит за символом  в определении дифференцируемой функции. Она дает приближенную формулу для вычисления функции. Формула Тейлора имеет вид: 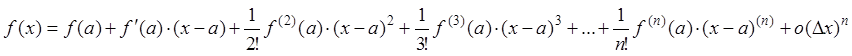. Символ называется n-факториалом – функция, которая для натуральных значений вычисляется по формуле: . Факториал можно также определить рекуррентной формулой: , 1!=1.

  Если приближение функции по формуле Тейлора известно, то из него можно прочитать значение производной в опорной точке.

Теорема Тейлора.

  Если в точке a функция  имеет производных до порядка n+1 включительно, то её значение вблизи точки x может быть представлено по формуле Тейлора.

Смысл структуры разложения Тейлора.

  В формуле Тейлора поправки к значению функции в опорой точке расположены по возрастанию порядка малости.

  Приближение функции по формуле Тейлора даёт представление функции, которая будет

Определение порядка малости дифференцированной функции.

  Дифференцируемая много раз функция называется бесконечно малой порядка n в точке a если её разложение по формуле Тейлора в этой точке начинается со слагаемого 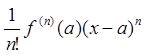. Путём деления на бесконечно малую порядка n, получается бесконечно большая того же порядка n.

Многочлены и их поведение.

  Многочлен порядка n – функция вида: , где a – константа.

  Утверждение 1. При  многочлен порядка n является бесконечно большой порядка n.

  Доказательство: .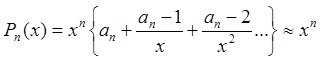

  Замечание: когда исследуем поведение функции при  бесконечно малые выстраиваем по степени переменной .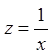

  Число b называется нулём (или корнем) многочлена порядка k, если многочлен можно записать в виде: .

  Утверждение 2. Вблизи корня кратности k, многочлен является бесконечно малой порядка k.

Лекция №7. Вычисление расстояния от точки до прямой. (25.09.00)

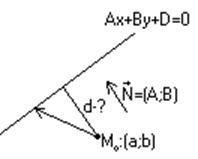Решение.

Берём любую точку на прямой. Проводим в неё вектор из точки (a;b) и ищем длину его проекции на вектор N.