Векторная алгебра. Анализ функции одной переменной. Равенства векторов и разновидность векторов. Дифференцируемая функция. Вычисление расстояния от точки до прямой, страница 4

              Обозначение сложных функций:

  Обычная:

  Ученая: - встройка идет справа налево.

  При работе со сложной функцией самое главное представить ее структуру, для этого удобно использовать следующие обозначения, например:

 

  .

Правило вычисления производной парной композиции.

Идея доказательства.

  Разворачиваем структуру функции и выписываем приращения:

 

  , где .

  Выписываем приращение всей функции через :

  - коэффициент при .

  Как частный случай производной сложной функции получаются правила вычисления производных дробей и обратных функций.

4. Вычисление производной дроби.

  .

  Применяем формулу производной произведения и сложной функции:

  , .

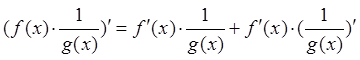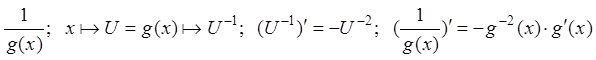5. Производная обратной функции.

  Обратная функция обозначается символом , поэтому для обозначения деления мы никогда не будем использовать показатель –1. Для обозначения деления будем использовать косую черту: .

  Главная формула определяющая обратную функцию: .

  Дифференцируем обе части используя правила вычисления сложной функции: , .

Пример: ; ; .

; , решаем полученное уравнение относительно, с использованием исходного тождества: .

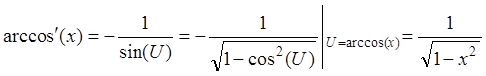Лекция №5. Смешанное произведение векторов. (18.09.00)

  Смешанное произведение векторов – это число вычисленное по тройке векторов.

  Обозначение:  или .

Правило вычисления.

  а) Бескоординатная формула.

 

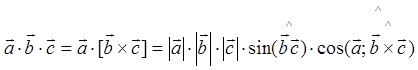
  б) Координатная формула.

.

Основные свойства смешанного произведения.

1.  Смешанное произведение меняет знак при перестановке сомножителей: .

2.  Модуль смешанного произведения равен объему параллелепипеда построенного на сомножителях . В параллелепипед вмещается 6 тетраэдров построенных на сомножителях:

Компланарность векторов.

  Векторы называются компланарыми, если они лежат в одной плоскости.

  Признак компланарности: смешанное произведение компланарных векторов равно нулю.

Ориентация тройки векторов.

  Тройка векторов  называется: правой, если  и левой, если . В частности правой является тройка векторов декартового базиса: , .

Применение смешанного произведения.

1.  Смешанное произведение применяется для вычисления объемов параллелепипедов и тетраэдров.

2.  Для записи условия компланарности в геометрических задачах.

Свойство линейности смешанного произведения.

  Смешанное произведение линейно по каждому сомножителю: .

Аналитическая геометрия на плоскости.

  Аналитическая геометрия – постановка и решение геометрических задач при помощи уравнений.

Прямые линии на плоскости.

  Чтобы задать линию, нужна опорная точка и вектор.

1.  Параметрическое уравнение прямой определяется опорной точкой и вектором, направленным вдоль прямой (направляющий вектор). 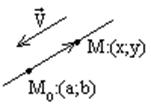Параметрическое уравнение прямой – условие коллинеарности: . Это условие можно записать и через координаты как система уравнений: 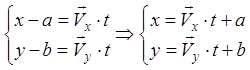. Таким образом очень удобно описывать прямолинейное движение.

2.  Общее уравнение прямой. Для записи общего уравнения прямой необходима опорная точка и вектор перпендикулярный прямой – нормальный вектор. 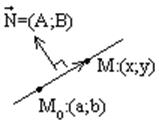Общее уравнение прямой – условие ортогональности нормального вектора на прямой.

^,  ,  .

Общее уравнение: .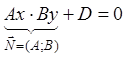

  Из общего уравнения необходимо научится добывать координаты нормального вектора.

  Примеры:

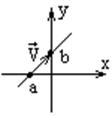Написать уравнение прямой, которая пересекает оси координат в точках (a;0), (0;b):

, , , , .

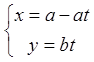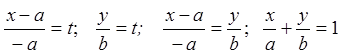  Необходимо найти координаты нормального вектора.

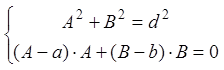
Взаимное расположение прямых линий.

  Задача. Дана пара уравнений описывающих прямые:

 

  .

  Если одно уравнение получается из другого умножением на константу – уравнения описывают одну и ту же прямую. Если это не так – уравнения описывают разные прямые.

  Определяем нормальные векторы к обоим прямым:

  ;  . Если , тогда прямые параллельны, в противном случае уравнения описывают пересекающиеся прямые.