Проектування гібридної інтегральної тонкоплівкової мікросхеми радіомікрофона, страница 6

а) плівковий конденсатор в перерізі; б) топологія плівкового конденсатора

(1 – верхня обкладка; 2 – діелектрична плівка; 3 – нижня обкладка;                 4 – підкладка)                                                

          Проводимо розрахунок для конденсаторів ;;

;  ;;

  при робочій напрузі (В).У відповідності до даних вибираємо матеріал діелектрика і обкладинок.

       Для цих конденсаторів найбільш підходящим є моноокис германію Наведемо його параметри:

- Діелектрична проникність = 8.

- Тангенс кута діелектричних втрат .

- Електрична міцність  Е_пр =(В/см)

-Температурний коефіцієнт ємності  .

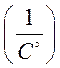Визначаємо  d_мін   діелектрика:

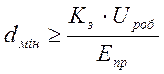,                                              (3.13)

де К_з – коефіцієнт запасу електричної міцності:   К_з = 3

U_роб = 9 В – робоча напруга.

Підставимо дані:

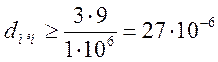(см).

Приймаємо (см).

Визначимо питому ємність конденсатора за виразом:

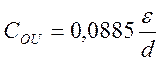 .                                              (3.14)

Розрахуємо питому ємність:

.

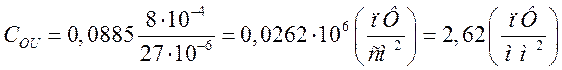Обрахуємо допустиму похибку  активної площі конденсатора за формулою:

,                                           (3.15)

де  - відносна похибка питомої ємності конденсатора;

 - відносна похибка ємності конденсатора після роботи;

 - відносна похибка старіння;

 - відносна температурна похибка;

,                                             (3.16)

   .

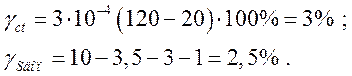        Обрахуємо питому ємність конденсаторів з урахуванням точності виготовлення за формулою:

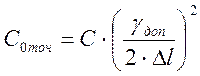,                                             (3.17)

де  - похибка довжини верхньої обкладинки ( = 0,01мм²).

Підставляємо дані:

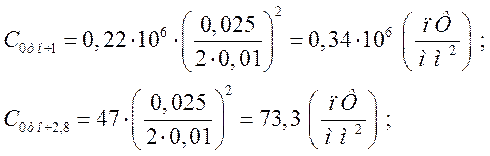
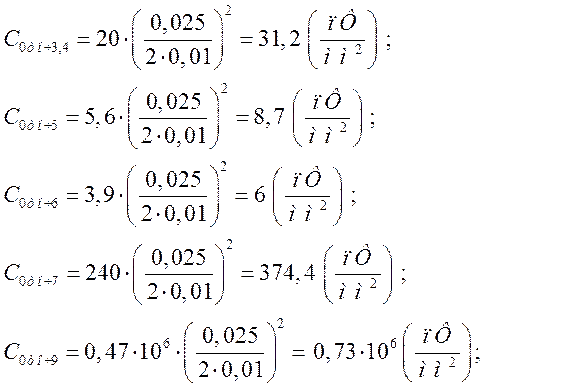
З обрахованих вище значень ємностей вибирається найменше

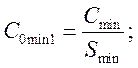                                                        (3.18)

.

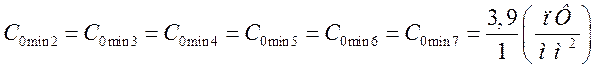де =1 мм² найменше значення площі плівки конденсатора.

Проведемо розрахунок геометричних розмірів конденсатора. Спочатку знайдемо коефіцієнт, що враховує крайовий ефект за формулою:

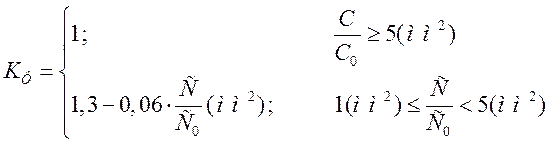                                     (3.19)

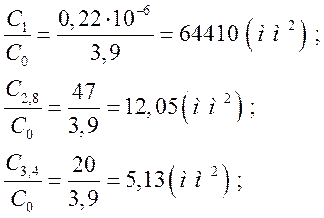
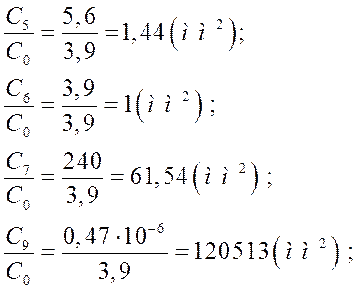
          З урахуванням значення 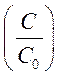, та формули 3.28 коефіцієнт що враховує крайовий ефект дорівнює:  для конденсаторів С1-С4, С7, С9; та 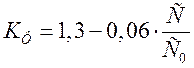 для конденсаторів С5, С6.

Визначимо площу верхньої обкладки конденсаторів.

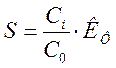                                            (3.20)

Підставимо до формули дані:

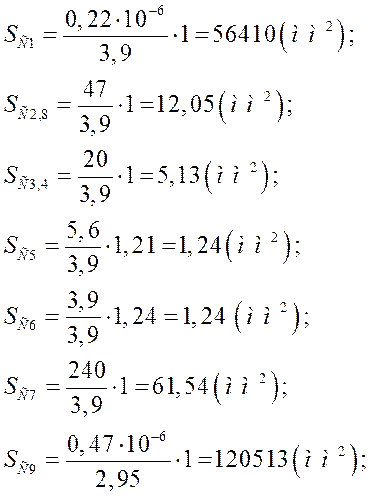
З розрахунків випливає, що С2 - С8  – плівкові; С1, С9 – навісні.

Обрахуємо розміри верхньої обкладки конденсаторів. Враховуючи, що конденсатори квадратної форми, задамось умовою, що довжина обкладинки дорівнює ширині.

.                                           (3.21)

Обрахуємо дані:

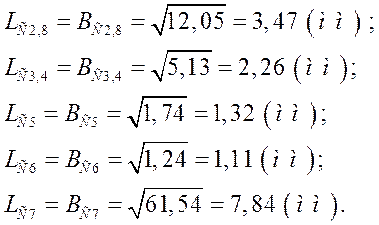
Визначимо розміри нижньої обкладки:

 ,                                            (3.22)

де q=0.1 – похибка ширини нижньої обкладинки.

Підставимо дані:

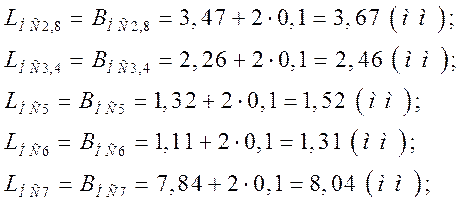
 Тепер знайдемо розміри діелектрика за формулою:

,                                         (3.23)

           де .

Підставимо дані:

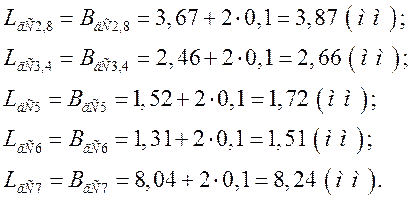
Визначаємо площу, яку займають конденсатори:

.                                            (3.24)

Тоді площа дорівнює:

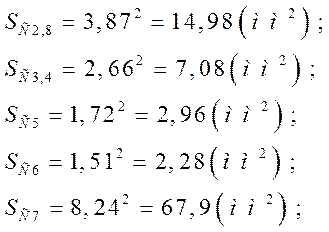
Проведемо перевірку розрахунку тонкоплівкових конденсаторів.    Конденсатор спроектований вірно якщо робочій тангенс кута діелектричних втрат  не перевищує  заданого . Також робоча напруженість електричного поля  не перевищує  діелектрика.

;                                            (3.25)

де tg δ_роб – робочий тангенс кута діелектричних втрат,

tg δ_роб= tg δ_діел+ tg δ_об;                                   (3.26)

де tg δ_діел і tg δ_об – тангенси кутів діелектричних втрат у діелектрика та обкладинках відповідно,

tg δ_об≈ωR_обС,                                       (3.27)

де R_об – опір обкладинок конденсатора;

     С – ємність конденсатора;

     ω – кутова частота,

R_об=ρ_sобК_ф,                                          (3.28)

де ρ_sоб=0.2  - питомий опір матеріалу обкладинок, в даному випадку алюмінію.

                                    Е_роб<E_{п р ,}                 (3.29)

 Е_роб= U_роб/d,                                         (3.30)

         де Е_роб – робоча напруженість електричного поля,

γ_sроб≤γ_sдоп.                                           (3.31)