Способы управления векторным преобразователем частоты вращения асинхронных электродвигателей, страница 5

Ток статора при идеальном холостом ходе –I₁₀ ( минимально возможный ток) может быть определен с помощью выражения:

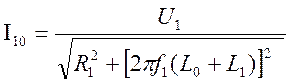                                                                                               (3.2)

где L_1, и L₀-соответственно индуктивности обмоток статора и намагничивания.

В общем случае при анализе характеристик частотно-регулируемого двигателя необходимо учитывать внутреннее сопротивление преобразователя частоты. Отсутствие данных о структуре и характеристиках преобразователя не позволяют их учесть в полной мере. Кроме того, вследствие  отсутствия  активных и индуктивных  значений сопротивлений обмоток двигателя, которые не приводятся в каталогах, корректный анализ характеристик двигателя  возможен  путём сравнения напряжений и токов для конкретных (фиксированных) частот. При этом  зависимость  характеристик двигателя  от частоты может быть определена в относительном масштабе.

Проведем анализ характера изменения момента вращения двигателя от частоты питания при постоянной  величине отношения  U₁ к  f₁. Пренебрегая в выражении 3.1 значением активного сопротивления обмотки статора  R₁, что правомерно для  «средних» и «больших» частот, где справедливо неравенство R₁ < x₁+x₂¹, и, заменяя сумму индуктивностей обмоток статора (L₁) и ротора (L₂¹)  через L формулу для момента можно представить в виде:

                                                     M  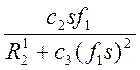                                                         (3.3),

где    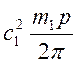=           ( 3.4),               c₁=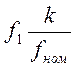     (3.5),                  c₃=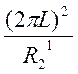       (3.6),

а параметр к – отношение выходного напряжения преобразователя к  входному напряжению (Рис. 4).

Произведение двух параметров f₁ и s можно представить в виде:              

                                        f₁s = 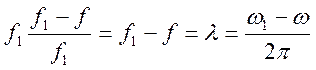                                          (3.7) ,

где    абсолютное скольжение, выраженное через разность угловых скоростей.

Значение  произведения  f₁s  зависит от величины момента сопротивления (растёт с увеличением нагрузки). При постоянном моменте сопротивления  максимальное значение  f₁-f  будет при  f_1.ном.  При уменьшении частоты питания двигателя ( f₁ значение f₁-f  так же  уменьшается (f₁-f. Таким образом, выражение для момента вращения (3.3) можно рассматривать как функцию одного аргумента .

Взяв в выражении 3.3 производную по параметру  () и прировняв её нулю, получим критическое значение параметра , при котором вращающий момент максимален:

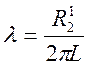                                                                                                                             ( 3.8).

Подставив эту формулу в выражение для момента  (3.3) получим значение для максимального момента:

                                                 M_max=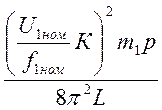                                                       (3.9).

Как и следовало ожидать, на величину максимального момента в первую очередь оказывает влияние величина выходного напряжения преобразователя, выраженная через параметр К

Из выражений 3.8 и 3.9 следует, что величина абсолютного критического скольжения: зависит от частоты  f₁ (с уменьшением  частоты величина абсолютного критического скольжения уменьшается, а жёсткость характеристики возрастает и наоборот).

 В общем случае предлагаемый алгоритм изменения  (выражение (1.5 )имеет некоторые ограничения при работе двигателя в области «низких частот», что влияет в том числе на пуск двигателя.

Например, предлагаемый алгоритм изменения напряжения  затрудняет пуск двигателя на частотах, приближающихся к нулю. Работа на частоте равной нулю вообще оказывается невозможной.

Кроме того,  вывод формул осуществлён при  допущении, что  в выражении 3.1-R₁=0.

Однако, на частотах, близких к пусковым  (f₁) влияние  R₁ по сравнению  значением         x₁+x₂¹-возрастает, что должно  привести к уменьшению момента вращения, а при некоторых условиях к невозможности реализации пуска.