Начертательная геометрия. Проекции с числовыми отметками: Методические указания и варианты заданий расчетно-графической работы для самостоятельной работы

Федеральное агентство по образованию

Государственное образовательное учреждение

высшего профессионального образования

«Кузбасский государственный технический университет»

Кафедра начертательной геометрии и графики

НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ

Проекции с числовыми отметками

Методические указания и варианты заданий расчетно-графической работы для самостоятельной работы  студентов  специальности 270205 «Автомобильные дороги и аэродромы»

Составители  Л. Е. Бахтина

                        Е. Г. Родина

Утверждены на заседании кафедры

Протокол № 5 от 4.12.2007

Рекомендованы к печати

учебно-методической комиссией специальности 270205

Протокол № 7 от 15.01.2008

Электронная копия находится

в библиотеке главного корпуса

ГУ КузГТУ

Кемерово 2008

1.  Цель и содержание задания

Цель настоящего задания – изучение студентами основных правил определения границ выемок и насыпей при проектировании строительных площадок и автодорог, получение навыков выполнения и оформления строительных чертежей.

В задании требуется:

1)  на заданной топографической поверхности разместить земляное сооружение с указанными уклонами откосов, определить границы земляных работ при строительстве сооружения;

2)  построить продольный профиль по оси дороги;

2.  Общие сведения

Параллельные проекции точек на любую плоскость проекций, сопровождаемые числами, определяющими удаление точек-оригиналов от их проекций, называются проекциями с числовыми отметками.

 В практике наиболее распространены прямоугольные проекции на горизонтальную плоскость проекций. Числовая характеристика заменяет собой фронтальную проекцию и определяет расстояние точек от плоскости H₀.

Проекции с числовыми отметками применяются в инженерно-строительном деле для изображения и проектирования на земной поверхности различных инженерных сооружений (дорог, аэродромов, котлованов, каналов, плотин и т.д.). В геодезии при помощи этих проекций изображается рельеф земной поверхности (планы в горизонталях).   

2.1.  Проецирование точки

Отметка в метрах записывается справа от обозначения проекции точки со знаком минус, если точка находится ниже плоскости нулевого уровня, и без знака, если выше плоскости Н₀  (рис. 1).

Рис. 1

Эпюр снабжается линейным масштабом, с помощью которого измеряются размеры на плане.

2.2.  Проецирование прямой

Длина проекции отрезка прямой на плоскость Н₀ называется заложением его (рис. 2).

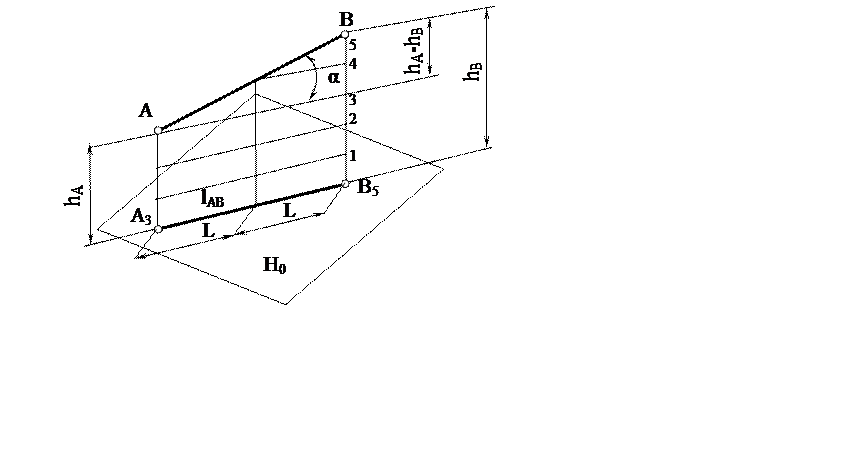
Рис. 2

А₃В₅ – заложение;        i=tg α – уклон;

α – угол наклона прямой к плоскости H₀   

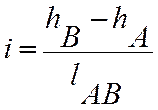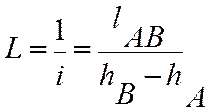 ;           – интервал

Интервалом прямой пользуются при градуировании ее проекции. Проградуировать проекцию прямой значит определить на ней точки с разностью отметок равной единице (рис. 3).

Рис. 3

2.3.  Две прямые

Для оценки взаимного положения прямых их проекции нужно проградуировать и сравнить отметки в точке пересечения проекций (рис. 4).

         

Рис. 4

Прямые пересекаются, если отметки в точке пересечения проекций окажутся равными.

Прямые скрещиваются, если отметки в точке пересечения проекций разные (рис. 4).

Прямые параллельны, если параллельны их проекции, интервалы равны, отметки возрастают в одном направлении (рис.5).

Рис. 5

2.4.  Плоскость

a –  угол падения плоскости

Рис. 6

Помимо известных способов задания плоскости ее можно определить еще масштабом падения (масштабом уклонов). Так называют градуированную проекцию линии наибольшего ската поверхности (рис. 6, 7).

Рис. 7

j – угол простирания плоскости

Линейный масштаб

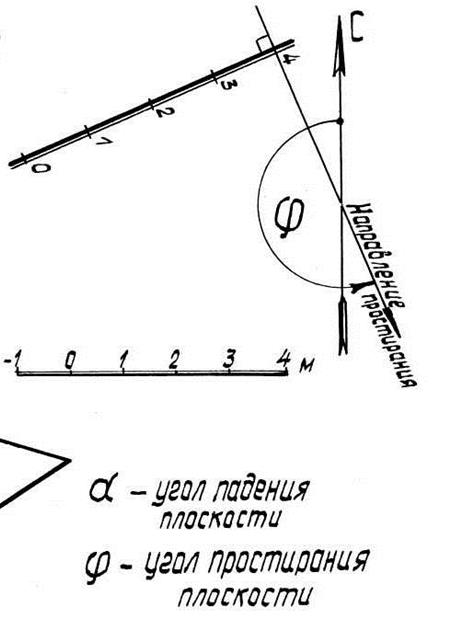
2.5.  Две плоскости

Для определения линии пересечения плоскостей используется тот же прием, что и в ортогональных проекциях (рис. 8).

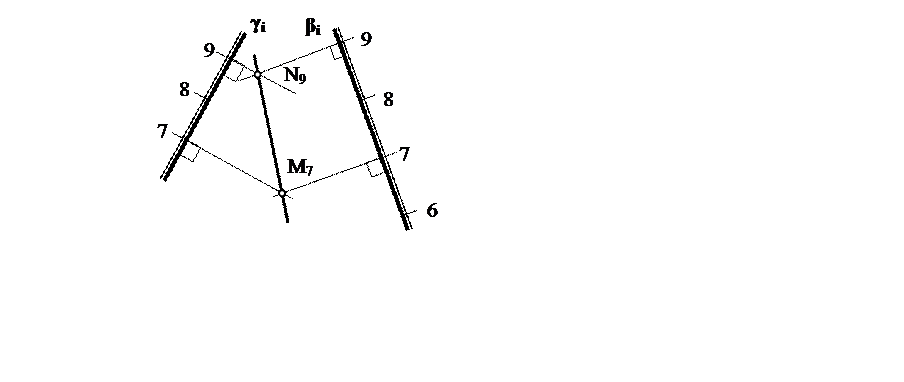
Рис. 8

На плане находят точки пересечения двух пар горизонталей заданных плоскостей с любыми одинаковыми отметками каждой пары.