3.3. Интерференционная функция Лауэ.
Выведенные выше геометрические условия возникновения дифракционной картины не предполагают различия интенсивности лучей, отражаемых от разных атомных плоскостей, которое отмечается на реальных рентгенограммах.
Найдем интенсивность рентгеновских лучей, рассеянных в произвольном направлении, пространственной решеткой кристалла. При элементарном рассмотрении задачи учитываем те упрощающие предположения, которые приведены в начале данного раздела.
Пусть кристалл имеет форму параллелипипеда,
элементарная ячейка которого определяется трансляционными векторами ![]() , а ряды,
параллельные
, а ряды,
параллельные ![]() ,
содержат N1, N2 и N3 узлов
(рассеивающих центров). Тогда число узлов в
кристалле равно N=N1N2N3. Суммарная амплитуда волны рентгеновского излучения, рассеянной кристаллом в данном
направлении, вычисляется по известным разностям фаз между волнами, рассеянными
разными центрами. Вычислим первоначально разность фаз между волнами, рассеянными двумя произвольно выбранными рассеивающими центрами. При этом удобно начало координат поместить в один из рассматриваемых центров
(рис.3.6).
,
содержат N1, N2 и N3 узлов
(рассеивающих центров). Тогда число узлов в
кристалле равно N=N1N2N3. Суммарная амплитуда волны рентгеновского излучения, рассеянной кристаллом в данном
направлении, вычисляется по известным разностям фаз между волнами, рассеянными
разными центрами. Вычислим первоначально разность фаз между волнами, рассеянными двумя произвольно выбранными рассеивающими центрами. При этом удобно начало координат поместить в один из рассматриваемых центров
(рис.3.6).
 Цусть
Цусть ![]() единичный вектор падающей волна.
Рассчитаем амплитуду вторичных волн в точке
наблюдения Q, находящейся на
расстоянии R от кристалла, настолько большем
расстоянии А1 А2 (или
единичный вектор падающей волна.
Рассчитаем амплитуду вторичных волн в точке
наблюдения Q, находящейся на
расстоянии R от кристалла, настолько большем
расстоянии А1 А2 (или![]() ), что можно считать
), что можно считать ![]() (дифракция Фраунгофера). Направление
распрастранения вторичных волн определим единичным вектором
(дифракция Фраунгофера). Направление
распрастранения вторичных волн определим единичным вектором ![]() . Тогда разность хода между волнами, рассеянными центрами А1 и А2 равна
. Тогда разность хода между волнами, рассеянными центрами А1 и А2 равна ![]() , а разность
фаз
, а разность
фаз ![]() где
где ![]() .
.
Уравнение падающей
волны в точке А1 имеет вид ![]() где
Е напряженность
электрического поля волны в точке А1; Е0 – амплитуда
волны в этой точке; ω –
круговая частота; t – время. Рассеянная волна рентгеновского
излучения, идущая от нулевого центра А1, имеет в
точке наблюдения Q с учетом рассеивающей способности центра Ф – амплитуду E0Ф/R и создает в ней возмущение
где
Е напряженность
электрического поля волны в точке А1; Е0 – амплитуда
волны в этой точке; ω –
круговая частота; t – время. Рассеянная волна рентгеновского
излучения, идущая от нулевого центра А1, имеет в
точке наблюдения Q с учетом рассеивающей способности центра Ф – амплитуду E0Ф/R и создает в ней возмущение
![]()
Суммарное возмущение Y, создаваеаое всеми рассеивающими центрами решетки кристалла, в предположении, что все центры рассеивают одинаково, будет равно
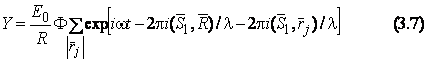
Суммирование проводится по всем
центрам решетки. Так как положение всех центров (узлов) предполагается
фиксированным, то расстояние от нулевого центра до j-того равно ![]() (m, n, p – целые числа).
(m, n, p – целые числа).
Выражение (3.7) можно представить в виде произведения трех сумм:
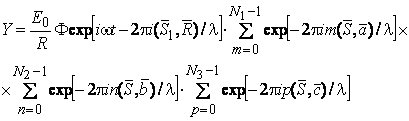 (3.8)
(3.8)
Каждая из этих сумм представляет собой сумму геометрической прогрессии и может быть переписана в виде
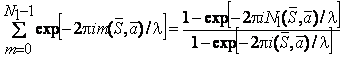 (3.9)
(3.9)
Экспериментально можно измерить не амплитуду Y, а интенсивность рассеянных лучей I. Интенсивность лучей, рассеянных кристаллом в направлении Q, является квадратом амплитуды Y, который может быть найден путем умножения Y на комплексно-сопряженнув величину YY*:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.