Интерференционная функция Лауэ. Атомный множитель, страница 2

.

Тогда        

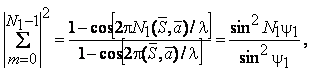               (3.10)

где .

Используя аналогичные преобразования, из (3.8) получим окончательное выражение для интенсивности в точке Q

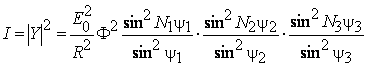             (3.11)

где ; .

Функция

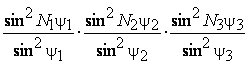                           (3.12)

называется интерференционной функцией Лауэ.

Математический анализ интерференционной функции Лауэ' позволяет определить направление интерференционного максимума по отношению к кристаллической решетке, а также учесть влияние размера кристалла на ширину максимума.

Рассмотрим выражение (3.12), оценив отдельно каждый из входящих в него сомножителей.

Когда  (где H – целое число или нуль), множитель 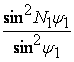 достигает максииума, равного по величине N₁². В этом можно убедиться путем двукратного применения к нему правила Лопиталя. Эти максимумы называются главными (рис.3.7).

Рис.3.7. График функции

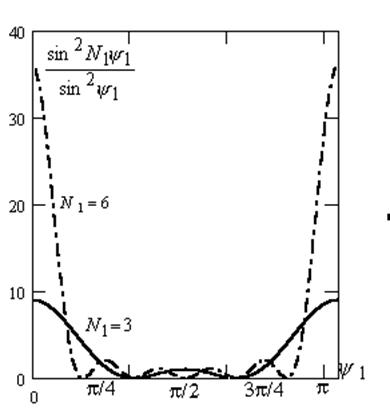
При непрерывном изменении ψ₁ от  до  функция 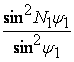 обращается в нуль, когда  где q=1, 2, 3,… (N₁-1). В этом случае числитель обращается в нуль, а знаменатель остается отличным от нуля. В интервале значений ψ₁, лежащих между  и , имеется (N₁-1) таких нулевых значений.

Между каждой парой нулевых значений 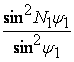 лежит побочный максимум этой функции. Его величина тем меньше, чем ближе значение ψ₁ к середине интервала  ÷ . Между парой главных максимумов находится (N₁-2) побочных максимума. Их положение определяется условием  где q=1, 2, 3,… (N₁-2). Если N₁ велико (на практике оно достигает по меньшей мере нескольких тысяч), то значения 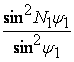ощутимы лишь при ψ₁ , очень близких к .

Интенсивность рассеяния рентгеновских лучей будет максимальна, когда каждый из сомножителей в выражении (3.12) достигает своего максимального значения, т.е. при выполнении условий

; ; ,   (3.13)

где Н, К , L – целые числа.

В этом случае она равна

               (3.14)

Условия (3.14) есть не что иное, как уравнения интерференции Лауэ

.