Интерференционная функция Лауэ. Атомный множитель, страница 3

Следует напомнить, что HKL - индексы интерференции Лауэ; они же определяют координаты узлов обратной решетки.

Подставим (3.13) в (3.14). Тогда

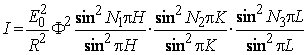               (3.15)

Условия дифракции, в форме Лауэ в данном случае означают, что координаты узла обратной решетки HKL должны быть целыми числами. При нецелочисленных значениях HКL уравнение (3.15) дает выражение для определения интенсивности в точке обратного пространства, лежащей между его узлами.

Таким образом, при решении дифракционных задач интенсивность рассеянного излучения сопоставляется с каждой точкой обратного пространства. Причем интенсивность может отличаться от нуля не только точно в узле обратной решетки, но и в некоторой области вблизи него, что можно интерпретировать как размытие узла. Действительно, рассеянное излучение обладает заметной интенсивностью в области HKL лежащей в пределах H±1/N₁; K±1/N₂; L±1/N₃ (см.рис.3.7).

Ширина дифрагированного максимума определяется шириной интерференционной функции в обратном пространстве, ширина которой в свою очередь определяется размерами кристалла, т.е. числом рассеивающих центров N₁, N₂, N₃ вдоль его ребер.

За рассеивающий центр в данном кристалле естественно принимать его элементарную ячейку, так как она есть тот элемент кристалла, который, будучи размноженным но трем трансляционным осям  дает представление о всем кристалле. Если в элементарной ячейке содержится один атом (примитивная решетка), то ее рассеивающая способность определяется рассеивающей способностью данного атома.

3.4. Атомный множитель

При выводе интерференционной функции предполагалось, что электроны атома сосредоточены в геометрической точке – узле пространственной решетки. При таком условии волны рентгеновского излучения, рассеянные в любом направлении всеми Z электронами одного и того же атома, совпадают по фазе и при взаимодействии амплитуды их суммируются, так что амплитуда излучения, рассеянного атомом, в Z раз больше амплитуды излучения, рассеянного единичный электроном. Однако в действительности электроны распределены по объему атома. Расстояния между электронами в атоме соизмеримы с длиной волны излучения. Поэтому лучи, рассеянные разными электронами одного и того же атома, могут различаться по фазе, и, следовательно, их амплитуды нужно складывать геометрически, с учетом разностей фаз. В результате этого амплитуда волны, рассеянной атомом, всегда меньше суммы амплитуд волн, рассеянных электронами атома.

Отношение f амплитуды волны, рассеянной атомом, к амплитуде волны, рассеянной электроном при тех же условиях (т.е. в том же направлении и при той же λ), называется атомной амплитудой рассеяния рентгеновских лучей. Так как интенсивность излучения пропорциональна квадрату амплитуды волны, то можно записать , где  – интенсивность лучей, рассеянных атомом;  – интенсивность лучей, рассеянных электроном. Принимая во внимание, что сомножитель 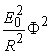 в (3.11) определяет интенсивность излучения рассеянного данным центром, т.е. атомом, получим

,

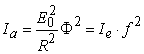откуда с учетом (2.5)

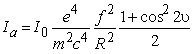
Величина  называется атомным множителем интенсивности.

Интенсивность излучения рассеянного кристаллом с примитивной решеткой в направлении удовлетворяющем условиям Лауэ, определится выражением