Усиление оптического излучения

2. УСИЛЕНИЕ ОПТИЧЕСКОГО ИЗЛУЧЕНИЯ

2.1. Прохождение оптического излучения через вещество

         Рассмотрим однородную оптическую среду, параметры которой неизменны во времени и пространстве.  Предположим, что среда идеально прозрачная, и ее показатель поглощения χ_п = 0 [м^–1]. Пусть эта среда  протяженностью L и сечением dS пронизывается вдоль оси z потоком квантов с частотой ν и спектральной плотностью мощности I_ν (рис. 2.1). При z = 0 падающий начальный поток P₀ = I_νdS = I₀dS, при z = L выходной поток определяется величиной P_L = I_L dS.

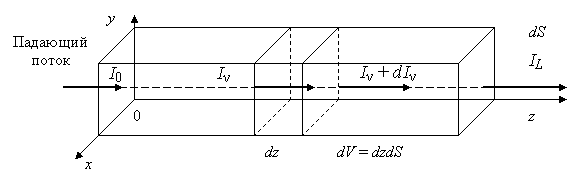
Рис. 2.1. Распространение излучения в слое вещества

Оценим изменение мощности ΔР_ν падающего излучения при прохождении  слоя вещества толщиной dz. Спонтанное и индуцированное излучения увеличивают поток квантов, вынужденное поглощение – уменьшает. С учетом этого ΔР_ν = Р_сп(ν) + Р_инд(ν) – Р_п(ν) = n₂dVg(ν)A₂₁hν + n₂dVg(ν)B₂₁ w_ν hν – – n₁dVg(ν)B₁₂w_νhν,  где объем dV = dS dz. В направлении оси z превалирует индуцированное излучение, поскольку спонтанное излучение – разнонаправленное – излучается равновероятно во все стороны и  им можно пренебречь. Поделив обе части выражения для ΔР_ν  на dS, перейдем к приращению плотности мощности и учтем, что B₁₂ = B₂₁, а плотность мощности для направленного излучения в вакууме  I_ν = c w_ν:

                        dI_ν = g(ν)B₂₁ hν с^–1 I_ν (n₂ – n₁) dz.                                   (2.1)

С учетом единиц измерения dz [м] и (n₂ – n₁) [м^–3] – разности концентраций частиц на верхнем и нижнем уровнях получим, что произведение первых пяти сомножителей в (2.1) должно выражаться в единицах площади [м²]. Это произведение называют сечением индуцированных переходов:

σ_инд  =  g(ν) B₂₁ hν с^–1.                                   (2.2)

         Для изменения плотности мощности в слое вещества окончательно получим

dI_ν = σ_инд (n₂ – n₁) I_ν dz.                                    (2.3)

         Входящие в  (2.3) величины σ_инд, I_ν и dz всегда положительны, следовательно, знак dI_ν  будет определяться только разницей  (n₂ – n₁).

2.2. Инверсия населенностей и активные среды

         Рассмотрим три случая возможного соотношения концентраций частиц на верхнем n₂ и нижнем n₁ энергетических уровнях.

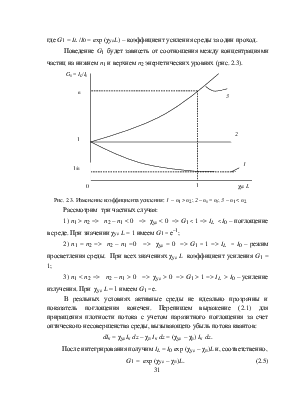
         1. Пусть n₁ > n₂. Тогда n₂ – n₁ < 0 и в соответствии с (2.3) dI_ν < 0, т. е. поток квантов в слое вещества ослабляется. Происходит поглощение излучения. Такие условия реализуются при термодинамическом равновесии, когда распределение частиц по энергетическим уровням подчиняется функции Больцмана:  n_i = g_i n₀ exp(– W_i/kT) (рис. 2.2). При ТДР концентрация n₁ частиц на нижнем энергетическом уровне всегда больше, чем концентрация n₂ на верхнем уровне. Поэтому равновесные среды всегда поглощают излучение.