Усиление оптического излучения, страница 2

2. Представим, что n₂ = n₁. Следова-тельно, Δn = n₂ – n₁ = 0 и dI_ν = 0. В этом слу-чае   среда идеально прозрачна, происходит просветление среды. На входе и на выходе потоки квантов одинаковые.      

3. Наконец, третий возможный вари-ант: n₂ > n₁ – нарушение равновесного распределения. Тогда  Δn = n₂ – n₁ > 0, и в слое   вещества   возникает прирост потока   Рис. 2.2. Распределения частиц:  квантов: dI_ν > 0 – происходит усиление опти-   1 – равновесное; 2 – неравновесное ческого излучения.

Формально условие n₂ > n₁ реализуется, если в функцию Больцмана подставить отрицательную абсолютную температуру (рис. 2.2, кривая 2), что является физическим абсурдом. Нарушение ТДР для всей системы осуществлено быть не может, но может быть реализовано выборочно для какой-то пары энергетических уровней. В этом случае говорят о создании инверсной (перевернутой) населенности уровней. Оптические среды, в которых возможно образование инверсной населенности, называют активными, усиливающими  или инверсными средами. Активные среды  (АС) могут быть созданы на основе газов, жидкостей, оптических кристаллов и диэлектриков или полупроводников.

Произведение сомножителей перед I_ν в (2.3) называется показателем усиления активной среды χ_ус = σ_инд (n₂ – n₁) [см^–1]. Если χ_ус > 0, поток на выходе среды больше, чем на входе.

В выражение (2.2) для σ_инд  входит дифференциальный коэффициент Эйнштейна B₂₁(ν) = g(ν)B₂₁, содержащий форм-фактор однородно или неоднородно уширенной спектральной линии. При расчете χ_ус конкретное значение g(ν) выбирается исходя из длины волны (частоты) усиливаемого излучения.  Для частного случая ν = ν₀, который называют центральной настройкой, g(ν) = g_max . Для однородного уширения g_{одн max} = 0,65/ Δν_одн, для  неоднородного ­ g_{нд max} = 0,9/Δν_нд. Поскольку числители в обоих случаях близки к единице, их часто опускают, полагая B₂₁(ν) = B₂₁/Δν_0,5.

2.3. Коэффициент усиления активной среды

Рассмотрим однородную прозрачную (χ_п = 0) оптическую среду протяженностью L, на которую падает поток квантов со спектральной плотностью мощности I₀. На выходе среды плотность мощности достигает значения I_L, определяемого  посредством интегрирования (2.3) после разделения переменных:

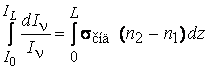   и далее          ,   откуда

I_L = I₀ exp (χ_усL) = I₀G₁ ,                                                    (2.4)              

где G₁ = I_L /I₀ = exp (χ_усL) – коэффициент усиления среды за один проход.

Поведение G₁ будет зависеть от соотношения между концентрациями частиц на нижнем n₁ и верхнем n₂ энергетических уровнях (рис. 2.3).

Рис. 2.3. Изменение коэффициента усиления: 1  – n₁ > n₂; 2 – n₁ = n₂; 3 – n₁ < n₂