Прямой аналитический расчет координат места судна

Вопрос №6

Прямой аналитический расчет координат места судна

Для омс необходимо измерить ,как минимум, два нп, и зная выражение нф, записать систему уравнений ни.

пример: на судне можем измерить два нп (расстояния) DA и DB до ориентиров A (xA,yA) и B(xB,yB). Имеем систему уравнений навигационных функций:

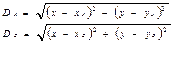    (1.37)

Теперь необходимо решить  систему (1.38) относительно неизвестных координат (x,y) , которые и являются координатами места судна.

Рассмотрим задачу определение места по двум пеленгам на плоскости.

Система уравнений с рис. 1.17 будет иметь вид:

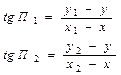                            (1.39)

где х₁ ,х₂, y₁, y₂ – координаты навигационных ориентиров.

Обозначив tgП₁ через Т₁,а tgП₂ через Т₁ ,х₀ =х, y₀ =y, запишем алгоритм решения системы: 

a)  Т₁(х₁–х₀)-y₁ = Т₂(х₁–х₀)–y₂;

b)  х₀=(Т₂х₂-Т₁х₁+y₁–y₂)/(Т₂-Т₁);

c)  y₀=(Т₁Т₂(х₂-х₁)+Т₂y₁–Т₁y₁)/(Т₂-Т₁);

d)  пусть П₁=30°, П₂=82°, тогда обсервованные прямоугольные координаты рассчитаем так:

e)  х₀=(tg(82°)*3-tg(30°)*8+5-9)/(tg(82°)-tg(30°)=1.95 мили

f)  y₀=(tg(30°)*tg(82°)*(3-8)+(tg(82°) *5-(tg(30°)*9)/(tg(82°)-tg(30°)=1.50 мили.

Аналитический вариант расчета координат места судна по двум линиям положения

Для определения места судна достаточно измерение двух навигационных параметров, так как поверхность на которой ищутся обсервованные координаты двухмерная (положение точки определяется двумя координатами).

Алгоритм расчета таков:

a.В момент времени t измеряются два навигационных параметра Uо1 и Uо2.

b.На этот же момент времени снимаются счислимые координаты xс,yс и на них рассчитываются счислимые навигационные параметры  Uс1 и Uс2.

c. На счислимые координаты рассчитываются коэффициенты линий положения aij , т.е. частные производные по навигационным параметрам от навигационных функций.

d.Правые части уравнений линий положения рассчитываются так: U1= Uо1 - Uc1, U2= Uо2 - Uc2.

e.Затем составляется система двух уравнений линий положения, которая может быть переписана в матричном виде, показанном ниже. Соответствующие матрицы имеют следующие названия: A- матрица коэффициентов линий положения, X- вектор неизвестных, U- вектор измерений (вектор свободных членов)

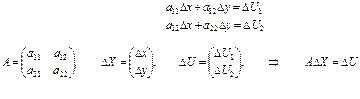    (2.6)

f.  Решение  системы уравнений линий положения (2.6)

                                                                                                    

g.  Если обозначить вектор счислимых координат, как X_c, а вектор обсервованных координат, как X_о , то можем записать: