5
1. РЕЗУЛЬТАТЫ измерений ПАРАМЕТРОВ СИГНАЛОВ ИСЗ .
1.1. Излучаемые ИСЗ и принимаемые на судне сигналы
1.1.1.Основные начальные понятия и принципы работы современных РНС предполагаются усвоенными по материалам учебника /1/. Целесообразно более детально остановиться на путях реализации в спутниковых РНС фундаментального требования – обеспечения в процессе радионавигационных определений точного знания о координатах передающих антенн каждого k-го ИСЗ при наличии реальных нестабильностей хранителей времени (ХВ).
В процессах фиксации (на ИСЗ) и измерения (в АП) временного положения сигналов СРНС участвуют три вида шкал времени (ШВ). Первая - шкала системного времени (ШВН), создается на наземном центре управления системой (ЦУС). В космической аппаратуре (КА) на каждом из ИСЗ реализуются другая разновидность – ШВК. Третья разновидность– ШВП - создается в аппаратуре потребителей (АП). Для формирования и ШВН и ШВК используются квантовые ХВ, в которых кварцевый генератор управляется и стабилизируется колебательными процессами например в атомно-лучевой трубке). Все КВ кроме кварцевого генератора содержат синтезаторы (СЧ) опорного непрерывного колебания (ОНК) и периодических видеоимпульсных напряжений (стробов или меток), используемых в КА для формирования:
1) необходимых шкал (меток) времени,
2) СВЧ несущей (вида sin wkt ) излучаемого сигнала,
3) огибающей (вида A(t)ºD(t)C(t)) излучаемого сигнала.
Заметим, что если – как в предыдущей строке – вводится некоторая величина без развернутого ее словесного определения, то такое определение делается в приведенном на стр. «списке обозначений основных величин и устройств».
Для упрощения изложения далее примеры инженерных решений будут в основном соответствовать отрытому каналу СРНС GPS, структура построения которого дана на рис.1.1
Режимы измерения в АП начинают функционировать (/1/, п.13.5) после окончания режима поиска (т.е. грубого совмещения соответствующих элементов сигнального D(т.) и Рис.1.1.
Здесь в верхнем канале формируется несущая путем умножения на 154 частоты ОНК, имеющего частоту fОНК=10,23 МГц. В выражении для огибающей Ak(t)ºDk(t)C(t) множители D(t) и C(t) представляют последовательности кодированных по знаку амплитуды (±1) прямоугольных видеоимпульсов единичной скважности, причем закон кодирования множителя D(t) зависит от номера спутника. Период первого (дальномерного) кода ТD=1000 мкс=1 мс. Длительность элементарных импульсов в GPS равна tЭ=ТD/1023, и элементарный сигнал содержит 1540 периодов несущей. Если С(t)=1 и форма элементарных видеоимпульсов описывается некоторой функцией, равной E(t)=1 при 0<t<tЭ и E(t)=0 при 0>t>tЭ, то в пределах TD огибающую излучаемого сигнала можно выразить как
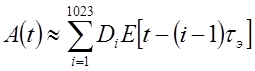 ,
,
где Di=±1 в соответствии с законом кода для i-го элемента в пределах периода кода.
В ГЛОНАСС tЭ=ТD/511. Длительность элемента кода С(t) сигналов существующих СРНС равна tЭС=20TD=20 мс.
Нижний канал рис.1 начинается приемником (РПК) сигналов служебного сообщения с ЦУС и КС. После его обработки в ЭВМ формируется служебное сообщение
6
данного ИСЗ, которое сохраняется долговременном запоминающем устройстве (ДЗУ).
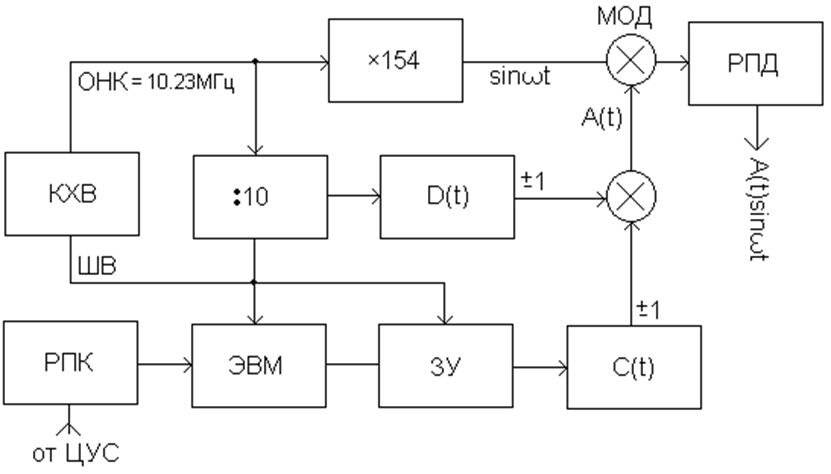 |
1.1. Структура формирования несущей и огибающей сигнала ИСЗ
В служебном сообщении передается и оцифровка tsk (пусть секундных) меток ШВК k-го ИСЗ. Если бы хранители времени ХВ всех ИСЗ были идеально «привязаны» к системному времени, то моменты появления меток ts всех КШВ и ЦШВ строго совпадали бы. При этом излучаемые сигналы (без учета особенностей поляризации и информационного кода) между соседними метками ШВ можно было бы аналитически выразить как
еk(t)=Аk(t-ts)sinwk(t-ts)=Аk(t-ts)sinYисз(t), (1.1)
причем мгновенная частота ВЧ заполнения, строго определяемая как скорость изменения текущей фазы, будет постоянна dYисз(t)/dt=wk.
В ГЛОНАСС огибающие Аk(t) сигналов всех ИСЗ содержат один и тот же множитель D(t), а в GPS неизменна несущая wk=wо, где wо/(2p)=154.10,23 МГц, Твч=2p/wо=0.635 нс, l»0,19 м.
Координаты передающей антенны k-го ИСЗ выражаются обсуждаемыми в разделе 2 функциями, аргументом которых является время t, отсчитываемое по ШВН. На моменты t= ts появления меток шкалы эти координаты выражаются как xks=xk(ts), yks =yk(ts), zks= zk(ts). Тогда расстояния rпк от каждого ИСЗ до приемной антенны пусть пока неподвижного АП с координатами X,Y,Z соответствуют равенства
rпк={[xk(t)-X]2+[yk(t)–Y]2+[zk(t)–Z]2}1/2,. (1.2)
где t=ts.
1.1.2. Из-за нестабильности ХВ ИСЗ относительно эталонного ХВ центра управления системой ЦУС передаваемая с k-го ИСЗ метка (с оцифровкой tsk) отстоит на некоторый интервал Dtk от момента t= ts-Dtk появления метки эталонной шкалы . Поэтому излучаемый сигнал вместо (1.1) примет вид
7
еk(t)=Ek(t-Dtk)sinwk(t-Dtk), (1.3)
а вместо (1,2) следует использовать формулу
rпк={[xk(ts-Dtk)-X]2+[yk(ts-Dtk)–Y]2+[zk(ts-Dtk)–Z]2}1/2, (1.4)
причем при малых Dtk координаты k-х ИСЗ на момент ts можно рассчитать, зная скорость изменения координат. Например, если vx(ts)= dxk(t)/dt при t=ts, то
xk(t)=xk(ts-Dtk)=xk(ts)-vx(ts)Dtk. (1.5)
Ориентировочно влияние Dtk можно оценить учитывая, что скорость ИСЗ близка 4м/мс. При неблагоприятном расположении ИСЗ и АП скорость изменения одной из координат будет иметь такой же порядок. При Dtk около миллисекунды погрешность расчета места ИСЗ может достигать порядка метров. Поэтому стремятся свести это расхождение к минимуму.
1.1.3. Поскольку расхождение ШВ двух ХВ неизбежно, то Dtk¹0 и возникает задача измерения значений Dtk и определения в каждом радиоканале «ЦУС-КА» функциональной зависимости Dtk=Dtk(t) от времени. Принцип измерения легко сформулировать, сначала представив, что НХВ и КХВ соединены коаксиальной неискажающей линией, задержка tл в которой существенно больше Dtk причем рядом и с НХВ и с КХВ имеются измерители интервала между «своей»и «чужой» метками. Пусть между НХВ и КХВ имеется служебная связь для взаимного обмена результатами измерений. Можно установить (рекомендуется самостоятельно), что полусумма и полуразность этих отсчетов будет равна соответственно t и Dtk. Такие измерения и выкладки можно выполнить и в реальных условиях с учетом откалиброванных аппаратурных задержек. Знание функции Dtk=Dtk(t) на ИСЗ необходимо для коррекции существенных отклонений временного положения ШВК (путем воздействия не на физические параметры квантового процесса генерации колебаний, а на цифровые синтезаторы частоты СЧ формирования ОНК и ШВК). Остаточная функция Dtk=Dtk(t) обычно аппроксимируется квадратичным трехчленом вида
Dtk=a0k+a1k(t-tsв)+a2k(t-tsв)2, (1.6)
где tsв- выбранные примерно через часовые интервалы метки системного времени. Коэффициент а1k пропорционален (рекомендуется доказать) разности периодов (частот) опорных колебаний ИСЗ и ЦУС, коэффициент а2k пропорционален скорости изменения а1. Численные значения коэффициентов a0k, a1k, a2k , содержащиеся в передаваемых с ИСЗ сигналах служебного сообщения, обеспечивают прогноз значений Dtk с погрешностью 1-3 нс при |t-tsв| < 0,65 ч. Если линейная скорость ИСЗ на орбите около 4 км = 4.109мм, то погрешность предвычисления местоположения ИСЗ на откорректированный момент излучения составит 4-12 мм. Что бы далее изложение особенностей алгоритмов бортовой аппаратуры не загружать деталями операций, связанных с учетом Dtk будем обычно полагать Dtk=0.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.